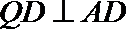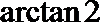- 真题试卷
- 模拟试卷
- 预测试卷
方程
正确答案
解析
令





考查方向
本题主要考查了指数函数与一元二次方程根的问题,换元思想与方程思想在近几年的各省高考题出现的频率较高,也是考试的重点。
易错点
1、本题易在换元后将其一元二次方程,求得负根,应舍去 。
知识点
以

正确答案
解析
根据圆与直线相切,得出

考查方向
本题主要考查了圆的标准方程、圆与直线的位置关系及其判定的综合能力。
易错点
本题易错在点到直线的距离公式的运算上
知识点
数列
正确答案
:
解析
利用等比数列求和公式


考查方向
本题主要考查了等比数列求和的基本运算
易错点
等比数列的求和公式忘记
知识点
等腰直角三角形的直角边长为1,则绕斜边旋转一周所形成的几何体的体积为 .
正确答案
解析
由已知得出几何体为圆锥,底面积为

考查方向
本题主要考查了旋转体的概念以及旋转体的体积
易错点
旋转体以谁为旋转轴直接导致图形的不同,是容易出错的
知识点
若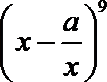
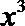
正确答案
1
解析
根据二项式的展开式,可得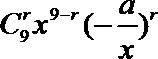
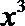
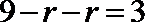
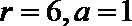
考查方向
本题主要考查了二项式系数的概念以及二项式展开的运算能力
易错点
容易混淆二项式系数与项的系数的概念
知识点
抛物线

正确答案
解析
根据抛物线





考查方向
本题主要考查了抛物线准线的定义与双曲线的渐近线的定义的综合应用
易错点
容易记错抛物线准线的定义
知识点
已知





正确答案
解析
由







考查方向
本题主要考查了矩阵的概念,三角函数图像与性质的综合应用
易错点
函数平移的对象是x,这是解决函数平移的问题的关键
知识点
两个三口之家,共4个大人,2个小孩,约定星期日乘红色、白色两辆轿车结伴郊游,每辆车最多乘坐4人,其中两个小孩不能独坐一辆车,则不同的乘车方法种数是 .
正确答案
48
解析
第一步:将两个小孩分别放在两辆车中,则是

考查方向
本题主要考查了排列组合的问题,也是常考题型
易错点
少算、多算是排列组合中最容易出错的问题
知识点
向量






正确答案
解析
由已知,得对




考查方向
本题主要考查了向量模的概念以及数量积的运算能力,也是常考题型
易错点
向量模的运算以及数量积的运算能力
知识点
已知:


正确答案
解析
由已知得,

考查方向
本题主要考查了复数和共轭复数的基本的概念以及基本运算,每年必考一题
易错点
复数的运算容易出错
知识点
数列

正确答案
:12
解析
由数列的前几项中可以发现每项的分子是是等差数列,分母刚好顺序相反,将上述数列分开,根据分母,1为一堆;1,2为一堆;1,2,3为一堆,1,2,3,4为一堆,依次下去求出规律,利用上述规律,求出
考查方向
本题主要考查了数列通项的定义以及对数列通项的观察能力,也是常考题型
易错点
数列规律不容易找到
知识点
已知直线





正确答案
:
解析
由直线

令



利用斜率定义,得
令

利用一元二次函数图像,求出

考查方向
本题主要考查了含参直线过定点问题,斜率的定义和函数的取值范围问题,也是常考题型
易错点
求直线过定点问题,求分式函数的取值范围容易出错,需要考虑范围
知识点
已知矩阵A=


正确答案
8
解析
利用矩阵乘积运算,得出
考查方向
本题主要考查了二阶矩阵的运算
易错点
矩阵AB运算,而不是矩阵BA运算,容易概念混淆
知识点
15.如图,该程序运行后输出的结果为( )
正确答案
解析
由

由于

考查方向
本题主要考查了程序题,是必考题型
易错点
计算需要小心,很容易出错
知识点
P是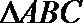
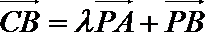
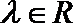
正确答案
解析
由已知,得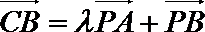
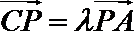
考查方向
本题主要考查了向量的基本运算以及平面几何的综合应用
易错点
向量基本运算需要仔细运算
知识点
若
正确答案
解析
能存在平面

因为平面

则直线

考查方向
本题主要考查异面直线的概念以及空间想象力,是常考题型
易错点
对空间想象力要求较高,需要一定的基础
知识点
王先生购买了一部手机,欲使用中国移动“神州行”卡或加入联通的130网,经调查其收费标准见下表:(注:本地电话费以分为计费单位,长途话费以秒为计费单位.)
若王先生每月拨打本地电话的时间是拨打长途电话时间的5倍,若要用联通130应最少打多长时间的长途电话才合算. ( )
正确答案
解析
由已知,王先生每月拨打本地电话的时间是拨打长途电话时间的5倍和条件,可知要用联通130应最少打400秒时间的长途电话才合算.
考查方向
本题主要考查分段函数以及资源最优化问题
易错点
少算了甲的费用
知识点
已知角







正确答案
解:(1)由

且

∴

∴
(2)由余弦定理得
,而∵
由


当且仅当
又


所以

解析
本题属于三角函数的基本问题,题目的难度是中等,本题的关键是:
(1)、向量的基本运算以及三角函数恒等变换的应用;
(2)、余弦定理与基本不等式之间的应用,一直是考试的热点问题,
考查方向
本题考查了向量运算、三角函数恒等变换、正弦定理和余弦定理的综合应用
易错点
向量的运算、余弦定理的应用,需要注意
知识点
如图,已知抛物线




















给出下列三个结论:
① 数列
② 对任意

③ 若


所有正确结论的序号是_____.
正确答案
① ② ③
解析
由题意,知数列







考查方向
本题主要考查抛物线的性质与数列的综合应用
易错点
抛物线性质与数列的结合处
知识点
在三棱锥
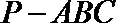
正确答案
解: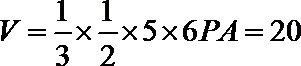
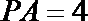
取PC的中点为D,连结AD,DQ,
则
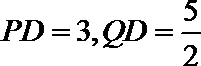
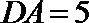
因为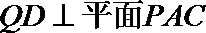
所以
所以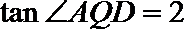
直线PB,AQ所成的角为
解析
本题属于空间几何体的基本问题,题目的难度是简单,本题的关键是通过添加辅助线找出异面直线PB,AQ所成的角,
考查方向
本题考查了空间几何体的体积与异面直线的综合应用
易错点
1、找异面直线PB,AQ所成的角容易出错
知识点
某市2013年发放汽车牌照12万张,其中燃油型汽车牌照10万张,电动型汽车2万张.为了节能减排和控制总量,从2013年开始,每年电动型汽车牌照按50%增长,而燃油型汽车牌照每一年比上一年减少
(1)记2013年为第一年,每年发放的燃油型汽车牌照数构成数列

(2)从2013年算起,累计各年发放的牌照数,哪一年开始超过200万张?
正确答案
(1)
当


当





(2)当

当
由

即
解得

解析
本题属于数列的应用题,题目的难度是中等,本题的关键是:
(1)、从所给的数列中找出规律,并求出两数列的通项公式;
(2)、再根据数列的通项公式的分段函数性质,求出各自的前n项和,最后利用函数的性质给出答案。这类数列的应用题型较为常见。
考查方向
本题考查了数列与函数之间的综合应用,特别是分段函数与数列的应用
易错点
1、分类讨论:



知识点
已知椭圆

(1)若已知


(2)求实数
(3)求

正确答案
(1)设

于是



因
所以,当

(2)由题意知


由


因为直线

所以,

①将



②由①②得



则 
且




所以
当且仅当
故

解析
本题属于解析几何的综合应用题,题目的难度是偏难,本题的关键是:
(1)、利用两点间的距离公式和点在曲线上的定义求出线段的范围;
(2)、利用设而不求法和中点坐标公式,求出m,b之间的关系,从而求出m的取值范围;
(3)、利用三角形面积公式和点到直线的距离公式,求出面积的表达式
考查方向
本题考查了椭圆与直线的位置关系、函数的取值范围问题的综合应用
易错点
1、




知识点
已知函数




(1)求证:数列
(2) 若




(3)若



正确答案
(1) 证:由题意
即
∴
∴
∵常数


∴数列


(2) 当


所以
因为

因而最小值为
(3) 由(1)知,


即

当



当




∵
∴当

∴

∴
综上所述,存在实数
解析
本题属于数列与不等式的综合应用题,题目的难度是偏难,本题的关键是:
(1)、利函数的性质求出数列的通项公式;
(2)、利用等比数列的求和公式求出前n项和的表达式,并求出最小值;
(3)、根据数学归纳法,分类讨论出k的取值范围。
考查方向
本题考查了数列的综合应用题,特别是数列与不等式之间的应用题
易错点
1、由