- 真题试卷
- 模拟试卷
- 预测试卷
1.已知集合


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.已知命题

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.在平面直角坐标系


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知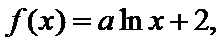
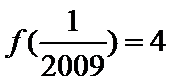
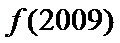
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6. 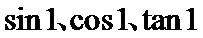
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.已知函数








正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.对于函数①


命题甲:
命题乙:

命题丙:

能使命题甲、乙、丙均为真的所有函数的序号是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知数列


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.已知数列


正确答案
1或
解析
解析已在路上飞奔,马上就到!
知识点
10.设

正确答案

解析
解析已在路上飞奔,马上就到!
知识点
11.求值:
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.已知函数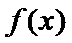
(1)对任意的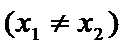

(2)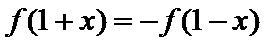
写出函数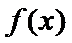
正确答案
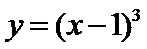
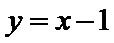
解析
解析已在路上飞奔,马上就到!
知识点
12.已知函数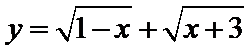
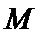

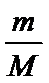
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.已知







正确答案

解析
解析已在路上飞奔,马上就到!
知识点
16.二次函数



正确答案

1当

2当

3当

4当
综上可知:
解析
解析已在路上飞奔,马上就到!
知识点
17.围建一个面积为360





(Ⅰ)将


(Ⅱ)试确定

正确答案
(Ⅰ)设矩形的的另一边长为
则
由已知
所以
(II)


即当x=24m时,修建围墙的总费用最小,最小总费用是10440元.
解析
解析已在路上飞奔,马上就到!
知识点
20.已知数列



(Ⅰ)求证:数列

(Ⅱ)求数列


正确答案
(Ⅰ)







即

(Ⅱ)由(Ⅰ)知,即



设
则
①


又





解析
解析已在路上飞奔,马上就到!
知识点
15.已知函数

(Ⅰ)求

(Ⅱ)将函数




正确答案
(Ⅰ)因为已知函数图象过点(







=

最小正周期
单调递减区间
(Ⅱ)由(Ⅰ)知
所以




所以当





解析
解析已在路上飞奔,马上就到!
知识点
19.已知函数



(Ⅰ)当

(Ⅱ)要使函数

(Ⅲ)若对(Ⅱ)中所求的取值范围内的任意参数



正确答案
(I)当

则

(II)

由

当

因此,函数


要使


(III)解:由(II)知,函数


由题设,函数



由(II),参数
要使不等式


综上,解得



解析
解析已在路上飞奔,马上就到!
知识点
18.已知函数
(I)若


(II)求
(III)若

正确答案
(Ⅰ)
∵
∴
(Ⅱ)
∵
①当


②当
由
∴
(Ⅲ)当
当


综上可知,若
解析
解析已在路上飞奔,马上就到!