- 真题试卷
- 模拟试卷
- 预测试卷
5.下列函数既是奇函数,又在区间
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.若函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.“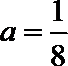
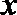
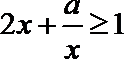
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.已知集合M={



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.如图,设点


点




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.已知定义域为







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.集合A可以表示为


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.若函数

正确答案
0
解析
解析已在路上飞奔,马上就到!
知识点
12.若


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13. 已知函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.已知关于


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.设曲线




正确答案
-2
解析
解析已在路上飞奔,马上就到!
知识点
17.定义在



①

②

③
④
其中正确的判断是__________(把你认为正确的判断都填上)
正确答案
①②④
解析
解析已在路上飞奔,马上就到!
知识点
19.已知函数
(1)求
(2)求函数的值域;
(3)判断函数的单调区间并证明。
正确答案
(1)
(2)(-1,1)
(3)R上递增
解析
解析已在路上飞奔,马上就到!
知识点
18.已知条件


(1)若

(2)若


正确答案
(1)

若
则
故
(2)
若
则 

故 
解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数
(1)判断函数
(2)求函数
(3)若关于



正确答案
(1)函数



∴
(2)当
若


若


再由

得


递减区间是

(3)由

当






∴
∴若方程

解析
解析已在路上飞奔,马上就到!
知识点
22.已知


(1)求

(2)若

(3)证明:

正确答案
(1)由题意
(2)由(1)知:
令h(x)=

h(x)≥0恒成立.
即


又
所以
(3)证明:证:lnx-x+1≤0 (x>0),
设
当x∈(0,1)时,k′(x)>0,∴k(x)为单调递增函数;
当x∈(1,∞)时,k′(x)<0,∴k(x)为单调递减函
∴x=1为k(x)的极大值点,
∴k(x)≤k(1)=0.
即lnx-x+1≤0,∴lnx≤x-1.
②由①知lnx≤x-1,又x>0,
解析
解析已在路上飞奔,马上就到!
知识点
20.已知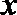
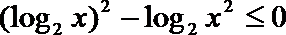
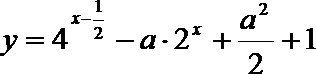
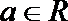
正确答案
解不等式 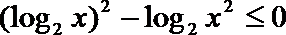
得 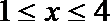
所以
当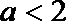
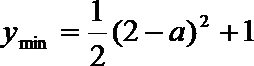
当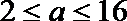
当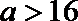
解析
解析已在路上飞奔,马上就到!