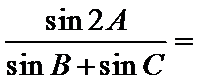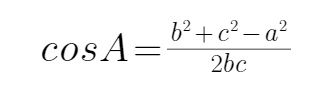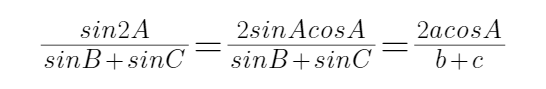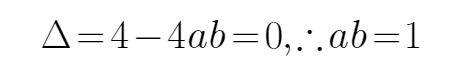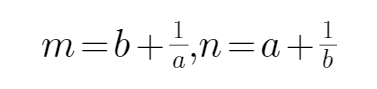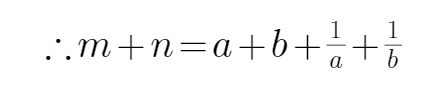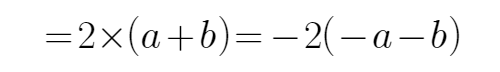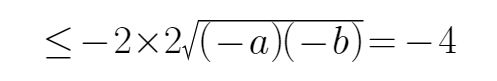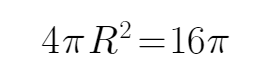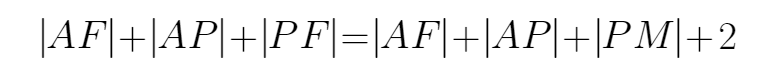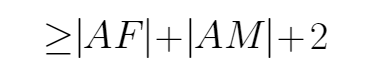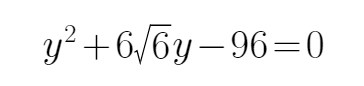- 真题试卷
- 模拟试卷
- 预测试卷
4．在三角形ABC中，角A、B、C的对边分别为
A
B
C
D
正确答案
知识点
5．已知
A
B
C
D
正确答案
知识点
6．执行如右图所示的程序框图．若输入
A
B
C
D
正确答案
知识点
9．已知a，b同号，二次不等式ax2+2x+b＜0的解集为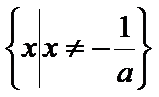
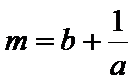
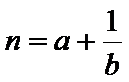
正确答案
知识点
1．设集合
A
B
C
D
正确答案
知识点
A
B
C2
D4
正确答案
知识点
3．已知
A
B
C
D
正确答案
知识点
7．三棱锥S-ABC及其三视图中的正视图和侧视图如图所示，则棱SB的长为
A
B
C
D
正确答案
知识点
8．已知抛物线
A
B
C2
D3
正确答案
知识点
11．某民营企业生产甲、乙两种产品，根据以往经验和市场调查，甲产品的利润与投入资金成正比，乙产品的利润与投入资金的算术平方根成正比，已知甲、乙产品分别投入资金4万元时，所获得利润（万元）情况如下：
该企业计划投入资金10万元生产甲、乙两种产品，那么可获得的最大利润（万元）是（ ）
A
B
C
D
正确答案
知识点
10．已知函数
A
B
C
D
正确答案
知识点
12．若函数
A
B
C
D
正确答案
知识点
11．某民营企业生产甲、乙两种产品，根据以往经验和市场调查，甲产品的利润与投入资金成正比，乙产品的利润与投入资金的算术平方根成正比，已知甲、乙产品分别投入资金4万元时，所获得利润（万元）情况如下：
该企业计划投入资金10万元生产甲、乙两种产品，那么可获得的最大利润（万元）是（ ）
A
B
C
D
正确答案
解析
因为甲产品的利润与投入资金成成比，所以可得关系式为
同理科求乙产品利润和投入资金的关系式为：
所以销售甲乙产品所的利润函数为：
则函数的导数
由导数大于0，可知
导数小于0，可知
所以当
考查方向
利用导数求函数的最值，实际问题与导数
解题思路
根据条件求出甲乙产品的利用表达式，分别求出投入甲乙两种产品的销售获得利润，利用换导数法求最大值
易错点
求导错误，对利润等相关概念理解不透彻
知识点
4．在三角形ABC中，角A、B、C的对边分别为
A
B
C
D
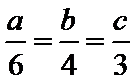
正确答案
解析
由题意可知设，
则a=6k,b=4k,c=3k
由余弦定理可得
=
由正弦定理可得
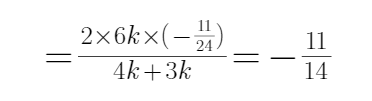
考查方向
正弦定理 余弦定理
解题思路
利用余弦定理可得cosA,再由正弦定理，化简可得
易错点
比例线段性质掌握不牢固
知识点
A
B
C2
D4
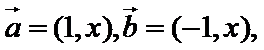
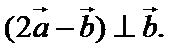
正确答案
解析
因为
所以
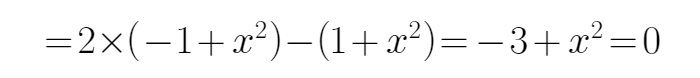
考查方向
平面向量数量积的运算
解题思路
利用两个向量垂直的性质，两个向量的数量积公式，求出x的值，然后可以得到向量的模
易错点
相关公式记忆混淆
知识点
3．已知
A
B
C
D
正确答案
解析
由题意可知，
解得
所以选A
考查方向
复数代数形式的乘除运算
解题思路
利用复数的代数形式的乘除运算及复数相等的性质可求得答案
易错点
计算错误，复数性质掌握不好
知识点
5．已知
A
B
C
D
正确答案
解析
作出可行域如上图，然后根据题意选出最值点，最后得到正确选项，因此此题选D
考查方向
简单线性规划
解题思路
作出不等式组对应的平面区域，利用目标函数的几何意义，利用数形结合即可得到结论
易错点
作图错误，求目标函数最值错误
知识点
1．设集合
A
B
C
D
正确答案
解析
集合
考查方向
子集与真子集
解题思路
求出集合N,从而判断出M,N的关系即可
易错点
集合的概念掌握不好
知识点
6．执行如右图所示的程序框图．若输入
A
B
C
D
正确答案
解析
循环前x=3,k=0，接下来x=8,k=1满足判断条件，
第1次 x=8+5=13,k=2,
第2次 x=13+5=18,k=3,
第3次 x=18+5=23,k=4,
第4次 x=23+5=28,k=5
满足判断框的条件退出循环，输出k=5
故选C
考查方向
程序框图
解题思路
计算循环中X和I的值，当X>23时满足判断框的条件，退出循环，输出结果K即可
易错点
程序框图循环结构判断错了
知识点
7．三棱锥S-ABC及其三视图中的正视图和侧视图如图所示，则棱SB的长为
A
B
C
D
正确答案
解析
由已知可知SC垂直面ABC，
且底面三角形ABC中AC=4，AC边上的高为
故BC=4,在直角三角形SBC中，由SC=4
可得
考查方向
简单空间图形的三视图
解题思路
由已知中的三视图可得SC垂直平面ABC，进而根据勾股定理得到答案
易错点
计算能力弱，空间立体感不强
知识点
8．已知抛物线
A
B
C2
D3
正确答案
解析
由一元二次不等式的解集可知方程有两个相等的实数根
所以
当且仅当
考查方向
一元二次不等式的解法
解题思路
根据一元二次不等式的解集和基本不等式求出M+N的最大值
易错点
不会解不等式，不能想到用基本不等式
知识点
9．已知a，b同号，二次不等式ax2+2x+b＜0的解集为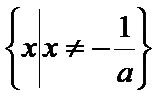
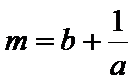
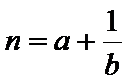
正确答案
解析
根据不等式的解集可以判断，方程有两个不等的实数根
所以
又
当且仅当a=b时，可得m+n的最大值为-4，所以选D
考查方向
一元二次不等式的解法
解题思路
根据一元二次不等式的解集得出根的判别式等于0，再利用基本不等式求出m+n的最大值
易错点
不能通过二次不等式的解集判断出方程有两个相等的实数根。
知识点
10．已知函数
A
B
C
D
正确答案
解析
由题意可知，
又
故
考查方向
两角和与差的正弦和余弦
解题思路
利用两角正弦公式化简成同角同名的三角函数，然后根据不等式，求出w的最小值
易错点
对三角函数的公式的变换掌握不好
知识点
12．若函数
A
B
C
D
正确答案
解析
由题意可知，当x>0，时，f(x)>0,所以2-m>0
故m<2.
因为f（x)由两个绝对值大于1的极值点，所以
所以选D
考查方向
函数的图象
解题思路
根据函数的极值点范围和函数值的符号判断
易错点
不会用导数的几何意义求解问题
知识点
13.将高三（1）班参加体检的36名学生，编号为：1，2，3，
正确答案
15
知识点
16．已知
正确答案
知识点
14．四面体ABCD的四个顶点都在球O的表面上，AB⊥平面BCD，三角形BCD是边长为3的等边三角形，若AB=2，则球O的表面积为_________．
正确答案
知识点
15．已知
正确答案
知识点
14．四面体ABCD的四个顶点都在球O的表面上，AB⊥平面BCD，三角形BCD是边长为3的等边三角形，若AB=2，则球O的表面积为_________．
正确答案
解析
取CD的中点E,连接AE,BE，因为四面体ABCD中,AB垂直平面BCD，三角形BCD是边长为3的等边三角形。
所以三角形ABC和三角形ABD全等，三角形ACD是等腰三角形
可求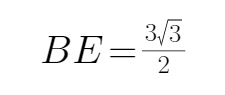
所以R=2，所以四面体ABCD外接球的表面积为：
考查方向
球的体积和表面积
解题思路
取CD的中点E,连接AE,BE，作出外接球的球心，求出半径，即可求出表面积。
易错点
不能作出正确的辅助线
知识点
13.将高三（1）班参加体检的36名学生，编号为：1，2，3，
正确答案
15
解析
样本间距为36/4=9，
所以另外一个编号为6+9=15，所以填15
考查方向
系统抽样方法
解题思路
根据系统抽样的定义，求出样本间隔即可
易错点
不理解什么是系统抽样
知识点
15．已知
正确答案
解析
有二项式展开的通项公式可得
所以令
所以原式=
考查方向
二项式定理；微积分基本定理
解题思路
由条件利用二项式展开式的通项公式求得a的值
再利用积分的运算性质、法则求出要求出的式子
易错点
展开式定理记忆混淆
知识点
16．已知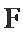
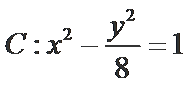
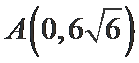
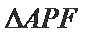
正确答案
解析
由题意可知，设M为左焦点，所以三角形APF的周长为
所以直线AM的方程为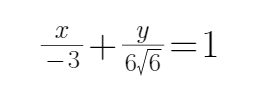
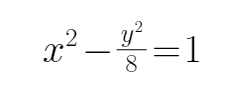
所以P的纵坐标为
所以三角形APF周长最小时，该三角形的面积为：
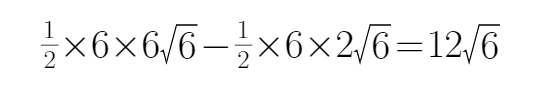
考查方向
双曲线的性质，双曲线的图像的特征
解题思路
利用双曲线的定义，确定APE周长最小时，求三角形的面积
易错点
对双曲线的性质和特征掌握不好
知识点
已知函数
24.当
25.若
正确答案
略
正确答案
略
已知单调递增的等比数列
17.求数列
18.若
正确答案
由
由
故
正确答案
某班同学
年龄段分组
[20，25）
[25，30）
[30，35）
[35，
[40，45）
频数
300
320
160
160
40
20
19.在答题卡上作出这些数据的频率分布直方图；
20.估计年龄段的“低头族”的平均年龄（同一组中的数据用该组区间的中点值作代表）；
21.从年龄段在[25，35）的“低头族”中采用分层抽样法抽取6人接受采访，并从6人中随机选取2人作为嘉宾代表，求选取的2名嘉宾代表中恰有1人年龄在[25，30）岁的概率．
正确答案
略
正确答案
设“低头族”平均年龄为
则
正确答案
略
如图，高为3的直三棱柱
22.求证：
23.求平面
正确答案
略
正确答案
略
选修4—1：几何证明选讲．
如图,已知
求证:
28.
29.
正确答案
略
正确答案
略
如图，点O为坐标原点，直线
26.若点O到直线
27.设点A是直线
正确答案
略
正确答案
略
已知单调递增的等比数列
17.求数列
18.若
正确答案
详见解析
解析
由
由
故
考查方向
求数列的通项公式
解题思路
根据条件，建立方程组即可求出数列的通项公式
易错点
数列通项公式记忆混淆
正确答案
详见解析
解析
考查方向
求数列的前N项和
解题思路
利用分组求和方法，对N讨论是奇数和偶数，即可得到答案
易错点
分类讨论时 有重漏
某班同学
年龄段分组
[20，25）
[25，30）
[30，35）
[35，
[40，45）
频数
300
320
160
160
40
20
19.在答题卡上作出这些数据的频率分布直方图；
20.估计年龄段的“低头族”的平均年龄（同一组中的数据用该组区间的中点值作代表）；
21.从年龄段在[25，35）的“低头族”中采用分层抽样法抽取6人接受采访，并从6人中随机选取2人作为嘉宾代表，求选取的2名嘉宾代表中恰有1人年龄在[25，30）岁的概率．
正确答案
详见解析
解析
根据频率分布表画出频率分布直方图即可
考查方向
频率分布直方图
解题思路
根据题意在分布直方图上标记
易错点
马虎大意
正确答案
详见解析
解析
设“低头族”平均年龄为
则
考查方向
平均数的计算
解题思路
根据平均数的定义即可求出
易错点
计算错误
正确答案
详见解析
解析
所有的可能情况为15种，恰有一人年龄在区间内的可能性有8种，所以概率为
考查方向
分层抽样 求等可能事件的发生的概率
解题思路
根据分层抽样的方法作出两个部分的人数，列举出所有试验发生包含的事件和满足条件的事件，根据等可能事件的概率公式，得到结果
易错点
计算能力弱，对数据敏感度不高
如图，高为3的直三棱柱
22.求证：
23.求平面
正确答案
详见解析
考查方向
直线与平面垂直的判定
正确答案
略
已知函数
24.当
25.若
正确答案
略
正确答案
略
选修4—1：几何证明选讲．
如图,已知
求证:
（1）
29.
正确答案
见解析
解析
PE切圆O于点E,
∠ECD=∠A+∠CPA
∠EDC=∠BEP+∠DPE
考查方向
考查与圆有关的比例线段问题
解题思路
先证明三角形中两角相等，则对应的两边相等
易错点
在角相等的转化过程中易错。
教师点评
本小问属于中档题，只要认真分析，可以得满分
正确答案
略
解析
同理△PDE
DE=CE
考查方向
本题考查了相似三角形的性质
解题思路
本题通过角的相等，转化为三角形相似，从而得到比例关系
易错点
相似比的转化过程易错
教师点评
本小题第二问较难，必须多角度转化比例关系才能得到结果