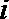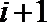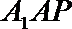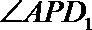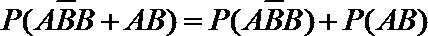- 真题试卷
- 模拟试卷
- 预测试卷
3.已知某几何体的三视图如图所示,则该几何体的体积为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.将甲,乙等5位同学分别保送到北京大学、复旦大学、中国科技大学就读,则每所大学至少保送一人的不同保送的方法数共有( )种。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.下列程序框图的功能是寻找使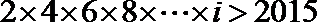

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.已知定义在










正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.复数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.已知全集
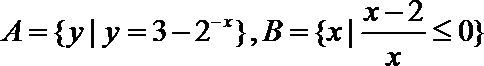
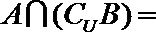
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知函数









正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.如图,棱长为


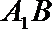
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.在直角坐标系中,点





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.过曲线









正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知


正确答案
135
解析
解析已在路上飞奔,马上就到!
知识点
12.已知圆
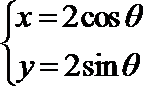
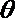

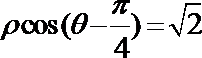

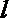
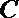
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.已知向量是单位向量

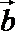
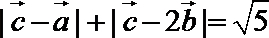
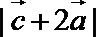
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.已知变量x,y满足

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.设





①存在


②存在







则称

①0为
②
③


④




正确答案
①③④
解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数
(Ⅰ)若

(Ⅱ)设


(Ⅲ)证明不等式:
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.在





(Ⅰ)求角
(Ⅱ)设




正确答案
解:(Ⅰ)因为
由正弦定理可得
由余弦定理可知

(Ⅱ)设



由正弦定理及

所以
所以
从而
由


即


此时

解析
解析已在路上飞奔,马上就到!
知识点
18.如图,直角梯形













(Ⅰ)证明:平面

(Ⅱ)求二面角
正确答案
(Ⅰ)略,
(Ⅱ)
解析
解析已在路上飞奔,马上就到!
知识点
19.在某校组织的一次篮球定点投篮训练中,规定每人最多投3次. 在A处每投进一球得3分;在B处每投进一球得2分. 如果前两次得分之和超过3分就停止投篮;否则投第三次. 某同学在A处的投中率
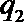
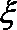
(Ⅰ)求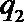
(Ⅱ)求随机变量

(Ⅲ)试比较该同学选择都在B处投篮得分超过3分与选择上述方式投篮得分超过3分的概率的大小.
正确答案
解:(Ⅰ)设该同学在A处投中为事件A, 在B处投中为事件B.
则事件A,B相互独立,且

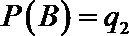
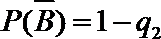
根据分布列知: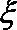

所以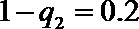

(Ⅱ)当



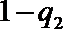

当

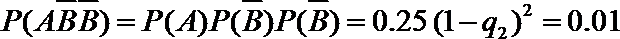
当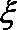

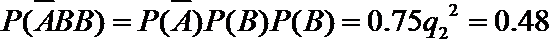
当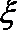
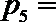
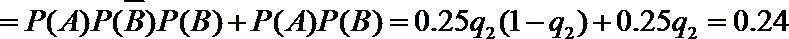
所以随机变量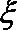
∴随机变量

(Ⅲ)该同学选择都在B处投篮得分超过3分的概率为

该同学选择(1)中方式投篮得分超过3分的概率为
由此看来该同学选择都在B处投篮得分超过3分的概率大.
解析
解析已在路上飞奔,马上就到!
知识点
20.定义:若两个椭圆的离心率相等,则称两个椭圆是“相似”的,如图,椭圆





(Ⅰ)求椭圆
(Ⅱ)过



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.已知数列




(Ⅰ) 求数列

(Ⅱ) 设



(Ⅲ) 设

正确答案
解:(Ⅰ)
(Ⅱ) 
(Ⅲ)由(Ⅰ),得

解析
解析已在路上飞奔,马上就到!