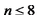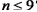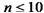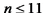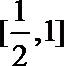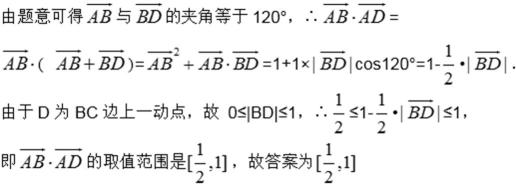- 真题试卷
- 模拟试卷
- 预测试卷
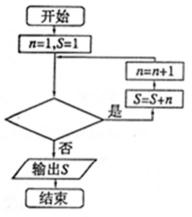
5.已知数列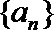
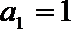
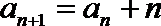
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知三棱锥的三视图如图所示,则它的外接球表面积为( )
正确答案
解析
由三棱锥的三视图可知中点位置即为球心,因为斜边长为
知识点
2.复数
正确答案
解析
解:可化为
知识点
7.已知函数




正确答案
解析
知识点
1.已知集合


正确答案
解析
由于集合M、N都是数集,所以


知识点
3.已知p:a>3,q:
正确答案
解析
知识点
4.设

①若



②若





③若

④若


其中正确命题的个数是( )
正确答案
解析
解:
①平行线中的一条垂直于一个平面则另一条也垂直于这个平面m⊥α则l⊥α正确.
②l可能属于α,所以不正确.
③l,m,n可能交于一点,所以不正确.
④n∥β∴n∥l∴l∥α∴l∥m∴正确.
知识点
6.已知向量


正确答案
解析




知识点
12.已知定义在





正确答案
解析
知识点
9.从0到9这10个数字中任取3个数字组成一个没有重复数字的三位数,则这个数能被 3整除的概率为 ( )
正确答案
解析
知识点
10.函数









正确答案
解析
知识点
11.已知双曲线







正确答案
解析
知识点
13.在边长为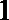
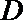
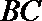
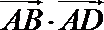
正确答案
解析
知识点
16.函数


(1)

(2)




下列函数中存在“和谐区间”的是__________.
正确答案
①③④
解析
知识点
14.(


正确答案
31
解析
x的系数为










知识点
15.抛物线


正确答案
解析
知识点
20.已知椭圆C:





(1)求椭圆方程;
(2)过椭圆的左顶点A作两条弦
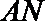






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.在汶川大地震后对唐家山堰塞湖的抢险过程中,武警官兵准备用射击的方法引爆从湖坝上游漂流而下的一个巨大的汽油罐.已知只有5发子弹,第一次命中只能使汽油流出,第二次命中才能引爆.每次射击是相互独立的,且命中的概率都是
(1)求油罐被引爆的概率;
(2)如果引爆或子弹打光则停止射击,设射击次数为ξ.求ξ的分布列及数学期望E(ξ).(结果用最简分数表示)
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21. 已知函数
(1)若函数

(2)求函数

(3)求证:对于任意的


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
请从22~24题中任选一题作答
22.<选修4—1:几何证明选讲>
如下图,AB、CD是圆的两条平行弦,BE//AC,BE交CD于E、交圆于F,过A点的切线交DC的延长线于P,PC=ED=1,PA=2.
(I)求AC的长;
(II)求证:BE = EF.
23.<选修4—4:坐标系与参数方程>
在直角坐标系







(1)若直线


(2)设


24.<选修4—5:不等式选讲>
设函数
(1)当
(2)若


正确答案

解析
解析已在路上飞奔,马上就到!
知识点
17.在等差数列








(1)求

(2)设数列




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.四棱锥






(1)求证:
(2)求二面角
正确答案

解析
解析已在路上飞奔,马上就到!