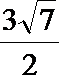理科数学南开区2013年高三试卷

精品

单选题
填空题
简答题

立即下载

理科数学热门试卷

X 查看更多试卷

试卷目录

1、单选题

2、填空题

3、简答题

真题试卷
模拟试卷
预测试卷

单选题本大题共8小题，每小题5分，共40分。在每小题给出的4个选项中，有且只有一项是符合题目要求。

题型：单选题

分值: 5分

2．已知条件，条件，且是的必要不充分条件，则实数a的取值范围是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

四种命题及真假判断

题型：单选题

分值: 5分

6．为了得到函数的图象，只需将函数的图象（）

A向左平移个长度单位

B向右平移个长度单位

C向左平移个长度单位

D向右平移个长度单位

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数解析式的求解及常用方法

题型：单选题

分值: 5分

7．平面向量与的夹角为，，则＝（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征

题型：单选题

分值: 5分

1．i是虚数单位，复数＝（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

虚数单位i及其性质

题型：单选题

分值: 5分

3．阅读下边的程序框图，运行相应的程序，当输入x的值为－25时，输出x的值为（）

A－1

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

程序框图

题型：单选题

分值: 5分

4．数列的前n项和为，则数列的前50项的和为（）

A49

B50

C99

D100

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

由数列的前几项求通项

题型：单选题

分值: 5分

5．二项式的展开式中的常数项是（）

A－28

B－7

D28

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

求二项展开式的指定项或指定项的系数

题型：单选题

分值: 5分

8．设是定义在R上的周期函数，周期为，对都有，且当时，，若在区间内关于x的方程＝0恰有3个不同的实根，则a的取值范围是（）

A（1，2）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的周期性指数函数的图像与性质对数函数的图像与性质函数零点的判断和求解

填空题本大题共6小题，每小题5分，共30分。把答案填写在题中横线上。

题型：填空题

分值: 5分

10．一个棱锥的三视图如图，则该棱锥的全面积（单位：cm2）为（）。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征

题型：填空题

分值: 5分

9．某校高中生共有2000人，其中高一年级560人，高二年级640人，高三年级800人，现采取分层抽样抽取容量为100的样本，那么高二年级应抽取的人数为（）人。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：填空题

分值: 5分

11．已知变量x，y满足约束条件，则的最大值为（）。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

不等式的性质

题型：填空题

分值: 5分

14．若不等式对任意都成立，则实数a取值范围是（）。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

不等式的性质

题型：填空题

分值: 5分

12．已知双曲线的左右焦点为，P为双曲线右支上的任意一点，若的最小值为8a，则双曲线的离心率的取值范围是（）。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

双曲线的定义及标准方程

题型：填空题

分值: 5分

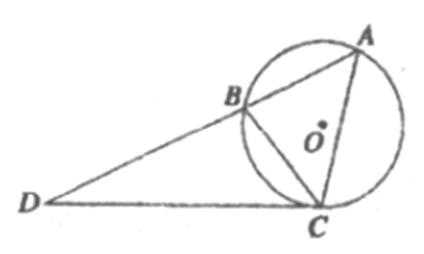
13．如图所示，圆O是△ABC的外接圆，过点C的切线交AB的延长线于点D，CD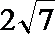＝，AB＝BC＝3，则AC的长为（）。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

弦切角与圆有关的比例线段

简答题（综合题）本大题共80分。简答应写出文字说明、证明过程或演算步骤。

题型：简答题

分值: 13分

15．已知向量，函数·

（1）求函数的最小正周期T及单调减区间

（2）已知分别是△ABC内角A，B，C的对边，其中A为锐角，且，求A，b和△ABC的面积S

正确答案

（1）

所以，最小正周期为

所以，单调减区间为

（2），

，

由得，解得

故

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征

题型：简答题

分值: 13分

17．如图，已知四棱锥E－ABCD的底面为菱形，且∠ABC＝60°，AB＝EC＝2，AE＝BE＝

（1）求证：平面EAB⊥平面ABCD

（2）求二面角A－EC－D的余弦值

正确答案

（1）证明：取AB的中点O，连接EO，CO

△AEB为等腰直角三角形

∴EO⊥AB，EO＝1

又∵AB＝BC，∠ABC＝60°，∴△ABC是等边三角形，

，又

∵EO⊥平面ABCD，又EO平面EAB，∴平面EAB⊥平面ABCD

（2）

以AB的中点O为坐标原点，OB所在直线为y轴，OE所在直线为z轴，如图建系则，，＝（0，2，0）

设平面DCE的法向量为，则，即，解得：

同理求得平面EAC的一个法向量为

，所以二面角A－EC－D的余弦值为

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征

题型：简答题

分值: 13分

16．张师傅驾车从公司开往火车站，途径4个公交站，这四个公交站将公司到火车站分成5个路段，每个路段的驾车时间都是3分钟，如果遇到红灯要停留1分钟，假设他在各交通岗是否遇到红灯是相互独立的，并且概率都是

（1）求张师傅此行时间不少于16分钟的概率

（2）记张师傅此行所需时间为Y分钟，求Y的分布列和均值

正确答案

（1）

（2）记张师傅此行遇到红灯的次数为X，则，，依题意，，则Y的分布列为

Y的均值为

解析

解析已在路上飞奔，马上就到！

知识点

相互独立事件的概率乘法公式离散型随机变量及其分布列、均值与方差

题型：简答题

分值: 13分

18．已知数列满足，

（1）证明：数列是等比数列，并求出的通项公式

（2）设数列的前n项和为，且对任意，有成立，求

正确答案

（1）由可得，

是以2为首项，3为公比的等比数列

（2）时，

时，

设

则

综上，

解析

解析已在路上飞奔，马上就到！

知识点

由数列的前几项求通项

题型：简答题

分值: 14分

19．设点P是曲线C：上的动点，点P到点（0，1）的距离和它到焦点F的距离之和的最小值为

（1）求曲线C的方程

（2）若点P的横坐标为1，过P作斜率为的直线交C与另一点Q，交x轴于点M，过点Q且与PQ垂直的直线与C交于另一点N，问是否存在实数k，使得直线MN与曲线C相切？若存在，求出k的值，若不存在，说明理由。

正确答案

（1）依题意知，解得，所以曲线C的方程为

（2）由题意设直线PQ的方程为：，则点

由，，得，

所以直线QN的方程为

由，

得

所以直线MN的斜率为

过点N的切线的斜率为

所以，解得

故存在实数k＝使命题成立。

解析

解析已在路上飞奔，马上就到！

知识点

定义法求轨迹方程

题型：简答题

分值: 14分

20．已知函数的最小值为0，其中。

（1）求a的值

（2）若对任意的，有成立，求实数k的最小值

（3）证明

正确答案

（1）的定义域为

，由，得，

当x变化时，的变化情况如下表：

因此，在处取得最小值，故由题意，所以。

（2）解：当时，取，有，故不合题意。

当时，令，即。

，令，得

－1。

i：当时，在上恒成立，因此在上单调递减，从而对于任意的，总有，即在上恒成立。

故符合题意。

ii：当时，，对于，，故在内单调递增，因此当取时，，即不成立。

故不合题意，

综上，k的最小值为。

（3）证明：当n＝1时，不等式左边＝右边，所以不等式成立。

当时，

。

在（Ⅱ）中取，得，从而

，

所以有

。

综上，。

解析

解析已在路上飞奔，马上就到！

知识点

简单复合函数的导数

理科数学 热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

理科数学热门试卷