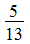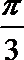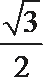- 真题试卷
- 模拟试卷
- 预测试卷
2.命题“∃x∈R,2x+x2≤1”的否定是( )
正确答案
解析
∵原命的否定为∀x∈R,2x+x2>1,∴取x=0,则20+02=1,故它是假命题.
知识点
5. 已知函数f(x)=
正确答案
解析
f(x+a)=sin(2x+2a-





知识点
6.已知抛物线y2=2px(p>0)的准线与曲线x2+y2-6x-7=0相切,则p的值为( )
正确答案
解析
整理圆方程得(x-3)2+y2=16∴圆心坐标为(3,0),半径r=4∵圆与抛物线的准线相切∴圆心到抛物线准线的距离为半径,即
知识点
8. 设O为坐标原点,F为抛物线y2=4x的焦点,A为抛物线上一点,若
正确答案
解析
F(1,0)设A(





知识点
10.若满足条件AB=

正确答案
解析
∵C=

∴由正弦定理得:
即


由题意得:当A∈(

所以

解得:

知识点
7.圆心在直线y=x上,经过原点,且在x轴上截得弦长为2的圆的方程为( )
正确答案
解析
由于圆心在y=x上,所以可设圆的方程为(x-a)2+(y-a)2=r2,将y=0代入得:x2-2ax+2a2=r2∴x1+x2=a,x1•x2=2a2-r2,∴弦长=|x1-x2 |=
知识点
3. 已知△ABC中,tanA=-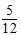
正确答案
解析
∵△ABC中,tanA=-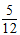
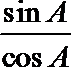

知识点
9.函数y=logax+1(a>0且a≠1)的图象恒过定点A,若点A在直线
正确答案
解析
当x=1时,y=loga1+1=1,
∴函数y=logax+1(a>0且a≠1)的图象恒过定点A(1,1),
∵点A在直线+-4=0(m>0,n>0)上,
∴
∴m+n=





当且仅当m=n=
知识点
1.设集合

正确答案
解析
A={x|

知识点
4. 若奇函数f(x)(x∈R)满足f(3)=1,f(x+3)=f(x)+f(3),则f等于( )
正确答案
解析
∵f(x+3)=f(x)+f(3),令x=-





知识点
12.已知点P是椭圆


正确答案
解析
如图,
当点P在椭圆与y轴交点处时,点M与原点O重合,
此时|
当点P在椭圆与x轴交点处时,点M与焦点F1重合,
此时|

∵xy≠0,∴|

知识点
11.函数f(x)的定义域是R,f(0)=2,对任意x∈R,f(x)+f ′(x)>1,则不等式ex·f(x)>ex+1的解集为( )
正确答案
解析
令g(x)=ex•f(x)-ex,则g′(x)=ex•[f(x)+f′(x)-1]∵对任意x∈R,f(x)+f′(x)>1,∴g′(x)>0恒成立,即g(x)=ex•f(x)-ex在R上为增函数,又∵f(0)=2,∴g(0)=1故g(x)=ex•f(x)-ex>1的解集为{x|x>0},即不等式ex•f(x)>ex+1的解集为{x|x>0}
知识点
13. 设不等式组所表示的平面区域为S,若A、B为区域S内的两个动点,则|AB|的最大值______.
正确答案
解析
作出不等式组对应的平面区域如图:


知识点
14.已知|a|=|b|=2,(a+2b)·(a-b)=-2,则a与b的夹角为________.
正确答案
解析
∵|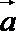
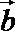

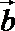
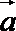
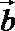
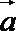
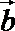

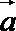
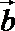
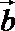
即cosθ=
知识点
16.函数f(x)=xex-a有两个零点,则实数a的取值范围是________.
正确答案
-
解析
∵函数f(x)=xex-a的导函数f′(x)=(x+1)ex,
令f′(x)=0,则x=-1
∵当x∈(-∞,-1)时,f′(x)<0,函数f(x)单调递减;
当x∈(-1,+∞)时,f′(x)>0,函数f(x)单调递增;
故当x=-1时,函数取最小值f(-1)=-e-1-a,
若函数f(x)=xex-a有两个零点,
则f(-1)=-e-1-a<0;即a>- 
又∵a≥0时,x∈(-∞,-1)时,f(x)=xex-a<0恒成立,不存在零点
故a<0综上,-
知识点
15.两个等差数列的前n项和之比为,则它们的第7项之比为________.
正确答案
3:1
解析
设这两个等差数列的前n项和分别为Sn,Tn,由题意知
知识点
17. 已知函数f(x)=2sinxcos(x+
(1)求函数f(x)的最小正周期;
(2)当
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18. 已知a、b、c分别为△ABC三个内角A、B、C的对边,

(1)求A;
(2)若a=

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
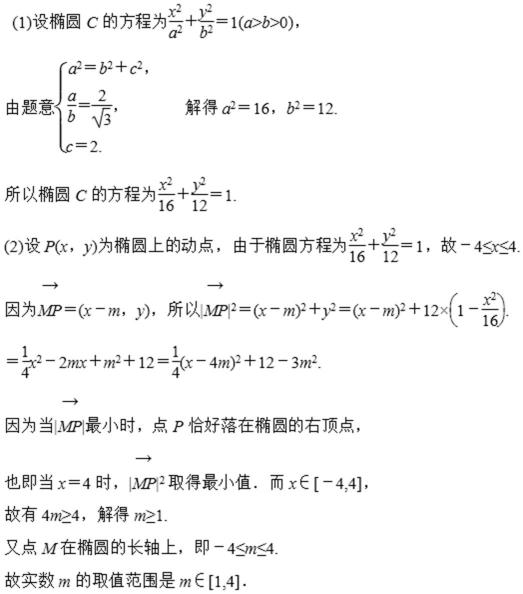
20. 椭圆C的中心在原点,一个焦点F(-2,0),且短轴长与长轴长的比是
(1)求椭圆C的方程;
(2)设点M(m,0)在椭圆C的长轴上,点P是椭圆上任意一点.当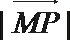
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.各项都为正数的数列{an},满足a1=1,
(1)求数列{an}的通项公式;
(2)求数列
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.点F为(1,0),M点在x轴上,P点在y轴上,且
(1)当点P在y轴上运动时,求N点的轨迹C的方程;
(2)设A(x1,y1)、B(x2,y2)、D(x3,y3)是曲线C上的三点,且


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
22.已知
(1)若


(2)当


(3)







正确答案
解析
解析已在路上飞奔,马上就到!