- 真题试卷
- 模拟试卷
- 预测试卷
5.已知函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知一个四棱锥的正视图和侧视图为两个完全相同的等腰直角三角形(如图示),腰长为1,则该四棱锥的体积为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.已知集合

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.下列命题中是假命题的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.一颗骰子连续掷两次,朝上的点数依次为

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.若不等式


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.设a,b,c为实数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.实数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.若直线



正确答案
− 1
解析
解析已在路上飞奔,马上就到!
知识点
10.(如图示)已知PA是圆O(O为圆心)的切线,切点为A,PO交圆O于B、C两点,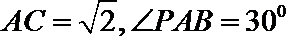
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.已知一个公园的形状如图所示,现有4种不同的植物(可以全种,也可以种一部分)要种在此公园的A,B,C,D,E这五个区域内,要求有公共边界的的两块相邻区域种不同的植物,共有( )种不同的种法.
正确答案
168
解析
解析已在路上飞奔,马上就到!
知识点
13.若数列


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.从集合A=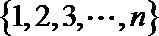
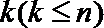
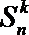
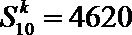
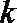
正确答案
4或7
解析
解析已在路上飞奔,马上就到!
知识点
11.用黄金分割法寻找最佳点,试验区间为[1000,2000],若第一个二个试点为好点,则第三个试点应选在( ).
正确答案
1236
解析
解析已在路上飞奔,马上就到!
知识点
16.已知向量



(Ⅰ)求函数
(Ⅱ)在







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.如图示,已知平行四边形ABCD和矩形ACEF所在平面互相垂直,AB=1,AD=2,
(1)求证:
(2)设二面角A—FD—B的大小为

(3)设点P为一动点,若点P从M出发,沿棱按照
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17. 某食品厂为了检查一条自动包装流水线的生产情况,随机抽取该流水线上40件产品作为样本,称出它们的重量(单位:克),重量的分组区间为


(1)根据频率分布直方图,求重量超过505克的产品数量.
(2)在上述抽取的40件产品中任取2件,设

(3)从流水线上任取5件产品,求恰有2件产品的重量超过505克的概率.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.对于函数






(1)求函数
(2)已知数列


(3)设



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.某种出口产品的关税税率t.市场价格x(单位:千元)与市场供应量p(单位:万件)之间
近似满足关系式:
价格为5千元,则市场供应量约为1万件;若市场价格为7千元,则市场供应量约为2万件.
(1)试确定k.b的值;
(2)市场需求量q(单位:万件)与市场价格x近似满足关系式:

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.设椭圆






(1)求椭圆C的方程;
(2)是否存在直线


(3)若AB是椭圆C经过原点O的弦, MN

正确答案
解析
解析已在路上飞奔,马上就到!