- 真题试卷
- 模拟试卷
- 预测试卷
1.集合


正确答案
解析
由





考查方向
本题主要考查了解不等式与集合的交运算,在近几年的各省高考题出现的频率较高,常与解不等式、函数的定义域、值域等知识点给合。
易错点
1、本题易在集合的交并补运算上出问题。
2、对集合的意义理解不到到导致出错。
知识点
2.在复平面内,复数
正确答案
解析
由

考查方向
本题主要考查了复数的运算与复数的几何意义,常考复数的运算、复数的相关概念(模、共轭复数、纯虚数、实部、虚部及其几何意义)。
易错点
本题易复数运算上出错。
知识点
3.已知向量



正确答案
解析
由


考查方向
本题主要考查了向量的垂直与模——向量的数量积运算,在近几年的各省高考题出现的频率较高,常单独命题或与解三角形、三角函数等知识点结合。
易错点
本题易在数量积运算上出错。
知识点
9.曲线y=ln(2x-1)上的点到直线2x-y+3=0的最短距离是( )
正确答案
解析
对函数y=ln(2x-1)求导得



考查方向
本题主要考查了导数的几何意义,同时考查了数形结合思想,此类题型在近几年的各省高考题经常出现,常考导数的几何意义及其应用。
易错点
在解题思想上的寻找上和对函数y=ln(2x-1)求导上。
知识点
5.已知某几何体的三视图如图所示,则该几何体的体积为( )
正确答案
解析
由三视图判断知此为四棱锥

考查方向
本题主要考查了由三视图还原成实物图再进行体积与表面积的计算,在近几年的各省高考题出现的频率较高,常是独立命题,求体积、表面积与棱长,也与函数结合求最值问题。
易错点
1、无法由三视图还原出实物直观图。
2、公式不熟悉导致出错。
知识点
6.已知圆的方程为
正确答案
解析
由垂径定理可知:当点(3,5)为弦中点时为最短弦


考查方向
本题主要考查了点圆关系,当点在圆内时,过此点的最长弦与最短弦。在近几年的各省高考题出现的频率较高,直线与圆的位置关系一般在小题里考,也常与线性规划和均值不等式联系。
易错点
对这个模型不太熟悉,即垂径定理的应用。
知识点
7.三棱柱ABC-A1B1C1中,底面是边长为
正确答案
解析
以A为坐标原点,AC的垂线为X轴,AC为Y轴,AA1为Z轴建立空间直角坐标第,进而点B坐标为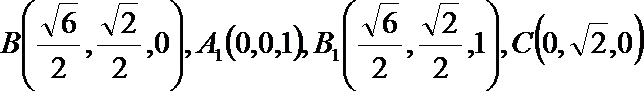
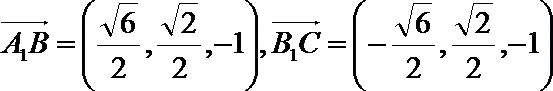
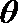
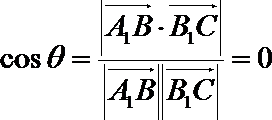
考查方向
本题主要考查了立体几何异面直线所成角问题,在近几年的各省高考题出现的频率较高。
易错点
1、本题如用传统方法易卡在作异面直线所成角。
2、用向量法易在一些点的坐标计算上难住。
3、异面直线所成角的范围。
知识点
8.按如图所示的程序框图运行后,输出的结果是( )
正确答案
解析
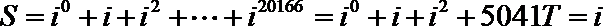
考查方向
本题主要考查了算法与复的结合,在近几年的各省高考题出现的频率较高,常以函数、数列、不等式、数学定义等知识点为背景,常考程序运行后输出,或已知目标填空等。
易错点
本题易在算法的目标上和最后n值是多少上出问题。
知识点
10.已知椭圆







正确答案
解析
设椭圆的点为




考查方向
本题主要考查了圆锥曲线的切线方程、面积计算和函数的最值问题,属于难度较大的题,常考求方程、离心率的值或范围、中点弦,面积等问题。
易错点
本题难在方程的合理假设与面积的计算易在集合的交并补运算上出问题。
知识点
4.已知递减的等比数列


正确答案
解析
解析已在路上飞奔,马上就到!
易错点
本题易运算上出错和审题上(忽略递减)导致导致出错。
知识点
11.如图,在平面直角坐标系中,AC平行于x轴,四边形ABCD是边长为1的正方形,记四边形位于直线x=t(t>0)左侧图形的面积为f(t),则f(t)的大致图象是 ( ).
正确答案
解析
当



考查方向
本题主要考查了实际问题对应的函数图象问题,在近几年的各省高考题出现的频率较高,常与长度、面积、体积为背景。
易错点
1、不理解图象代表的意义。
2、解决问题的切入点不合理或找不到切入点。
知识点
12.若





正确答案
解析
由方程













考查方向
本题主要考查了数形结合思想、反函数与函数的零点问题,在近几年的各省高考题出现的频率较高,属于能力要求较高的题目。
易错点
1、看不懂题目意思。
2、无法解出

知识点
14.
正确答案
解析
由题设知:
考查方向
本题主要考查了二项式展开式及二项式系数的概念。
易错点
本题必须注意二项式系数与系数的区别,还有就是题目要求写出此项,忽视则会出现错误。
知识点
16.已知等差数列





(1)
(2)
(3)
(4)当

(5)
其中正确的有 (把你认为正确的说法都写上)
正确答案
(1)(2)(4)
解析
由
















考查方向
本题主要考查了函数与数列的联系及等差数列的公式与性质。
易错点
不知道如何处理这个式子
知识点
20.已知抛物线





(1)若线段


(2) 若



正确答案
(1)
(2)
解析
本题属于圆锥曲线的基本问题,题目的难度是逐渐由易到难,
(1)由直线的参数表示出点
(2)根据弦长公式求出

(1)法一:
设



(1)当


(2)当

综上:
(1)法二:

设




(2)

考查方向
本题考查了求轨迹方程的方法、中点弦的处理方法、弦长公式及面积问题,常见求轨迹方程的方法有直译法、定义法、相关点法及参数法。圆锥曲线常见的问题有弦长、中点、面积、角度和“定”问题——定点、定线和定值。
易错点
1、求轨迹方程方法不熟练和点差法如何处理中点弦。
2、含参运算不正确导致出错。
知识点
13.已知

正确答案
解析
由题设知:
考查方向
本题主要考查了由函数的解析式求函数值的问题。
易错点
本题必须注意自变量所在范围的问题,忽视则会出现错误。
知识点
15.如果实数


正确答案
25
解析
可行域和初始线如图所示,当平行移动经过点

考查方向
本题主要考查了线性规划求线性目标函数的最值问题,常考的还有斜率型、距离型、函数型。
易错点
作出可行域,还有就是如何衡量最大和最小,忽视则会出现错误。
知识点
18.某单位考勤制度为早中晚刷脸3次,在规定时间内刷脸3次标记为绿色,刷脸2次标记为蓝色,刷脸1次标记为橙色,刷脸0次标记为红色,若标记为橙色,蓝色,红色需要填写申辩说明理由,现有前一天的考勤记录报表显示为甲办公室共计4人,其中标记红色1人,绿色2人,蓝色1人.乙办公室共计3人,其中标记橙色1人,绿色2人.现从甲乙两个办公室各任意抽取2人.
(1)求抽取的4人标记均为绿色的概率;
(2)若标记为红色,蓝色,橙色的人需要提交申辩,设所抽取的4人需要填写申辩的人数为

正确答案
(1)
(2)分布列为
期望为
解析
本题属于古典概型的常见题型,题目的难度是比较稳定,属于中档偏易题,
(1)直接计算出基本事件总数及符合所求的基本事件数;
(2)分析
(3)列出分布列,求出期望。
(1)设“抽取的4人标记均为绿色”为事件

(2) 





易错点
审题不清和考虑不全面导致出错。
知识点
19.多面体ABCDEF中,AF⊥平面ABCD,DE⊥平面ABCD,AF=2,AB=AD=
(1)求线段DE的长度;
(2)求二面角B-EF-D的大小;
正确答案
(1)DE=1;
(2)
解析
本题属于立体几何中的基本问题,题目的难度是逐渐由易到难,
(1)建好空间直角坐标系后,求出各点坐标;
(2)设出点E的坐标,再用共面定理求解出点E的坐标,再求出DE长。
(3)求出法向量再算出夹角。
(1)解:连接AC、BD,△ABD中,AB=AD=

△BCD中,BC=DC=1,∴∠BDC=30o
∴∠ADC=90o,即DA⊥DC
∵DE⊥平面ABCD,∴DA、DC、DE是两两垂直
以点D为坐标原点,如图建立空间直角坐标系D-xyz,则
点A(



∴
∵B、C、E、F四点共面,∴



(2)∵


∴取平面DEF的一个法向量

∴二面角B-EF-D的余弦值为
考查方向
本题考查了空间向量在立体几何中的应用,如何体现四点共面及二面角的计算,常见的问题有证明类——平行与垂直的证明;计算类——角度(线线角,线面角,二面角);长度(线度、点面、线面、面面距离)
易错点
1、遗忘共面定理导到出错;
2、二面角与法向量夹角之间是相等还是互补的判断。
知识点
21.
(1)当

(2)若

正确答案
(1)增区间

(2)
解析
试题分析:本题属于导数应用中的基本问题,题目的难度是逐渐由易到难,
(1)直接按照步骤来求
(2)要注意对参数的讨论
(3)涉及恒成立问题,转化成求函数的最值,这种思路是一般解法,也常采用“分离参数法”.涉及对数函数,要特别注意函数的定义域.
(1)当




解:
令

① 当


又
② 当

令

令


又


考查方向
本题考查了利用导数求含参数的函数单调区间,及恒成立问题的处理,最常用的方法是最值法和“分离参数法”
易错点
1、忽略函数的定义域导致出错。
2、第二问中的易丢对a的分类讨论。
知识点
17.
(1)求
(2)若


正确答案
(1)
(2)
解析
本题属于三角恒等变形和解三角形的基本问题
(1)直接按照步骤来求
(2)要注意观察,然后合理地选择公式来解题。
(1) 




(2)



考查方向
本题考查了三角函数的基本公式即:诱导公式、同角关系式、两角和差公式和二倍角公式在化简中的应用,内角和定理、正余弦定理在解三角形的应用;
易错点
1、对
2、根据条件合理选择定理来解三角形。