- 真题试卷
- 模拟试卷
- 预测试卷
1.已知全集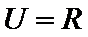
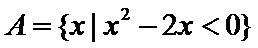
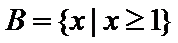
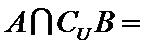
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.若点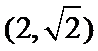
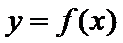
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.把函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.直线方程
正确答案

解析
解析已在路上飞奔,马上就到!
知识点
8.阅读如图所示的流程图,则该程序输出的结果是( ) .
正确答案
5
解析
解析已在路上飞奔,马上就到!
知识点
11.在直角坐标系






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.已知向量





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.若


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.正三棱柱



正确答案
8
解析
解析已在路上飞奔,马上就到!
知识点
9.已知


①若

②若

③若

④若

其中正确的命题是(填上所有正确命题的序号)( ).
正确答案
① ④
解析
解析已在路上飞奔,马上就到!
知识点
13.投掷两颗骰子,得到其向上的点数分别为m和n,则复数(m+ni)(n-mi)为实数的概率为( ).
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.已知







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.若

正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
10.设等差数列



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.若关于x,y,z的线性方程组增广矩阵变换为


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.下列所给的四个命题中,不是真命题的为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.已知数列






















正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.命题甲:实数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.设6张卡片上分别写有函数





(1)现从盒子中任取两张卡片,将卡片上的函数相加得一个新函数,求所得函数是奇函数的概率;
(2)现从盒子中进行逐一抽取卡片,且每次取出后均不放回,若取到一张记有偶函数的卡片,则停止抽取,否则继续进行,求抽取次数
正确答案
解:(1)记事件A为“任取两张卡片,将卡片上的函数相加得到的函数是奇函数”,则
(2)



故ξ的分布列为



解析
解析已在路上飞奔,马上就到!
知识点
21.已知点P(4,4),圆C:

(1)求m的值与椭圆E的方程;
(2)设Q为椭圆E上的一个动点,求
正确答案
(1)点A代入圆C方程,得
圆C:

即


当k=

当k=

2a=|AF1|+|AF2|=

椭圆E的方程为:
(2)


∵


所以,


解析
解析已在路上飞奔,马上就到!
知识点
22.已知函数
(1)设

(2)关于





(3)证明:当




正确答案
(1)函数定义域




(2)







即




(3)

以下证明,对


不等式
反之,由

因为


这说明
这样,不等式
即
∴ 

解析
解析已在路上飞奔,马上就到!
知识点
23.已知数集





(1)分别判断数集


(2)求


(3)由(2)及通过对

正确答案
(1)由于



由于








(2)∵




从而
当




从而



故数列
(3)命题一:对于一切大于或等于3的奇数


证明:由(2),不妨设





因为







第1组:

第2组:

第3组:

第


上一组的第2项总大于下一组的第1项,再注意到
第1组的各数从左到右依次为:
第2组的各数从左到右依次为:
第3组的各数从左到右依次为:
第

于是,有
由(﹡),




成等比数列.
命题二:对于一切大于或等于6的偶数


证略(同命题一的证明类似)
命题三:对于一切





(证略)若学生指出:当


例如数列

解析
解析已在路上飞奔,马上就到!
知识点
19.在




(1)求角
(2)若

正确答案
(1)由已知等式得:

(2)
解析
解析已在路上飞奔,马上就到!