- 真题试卷
- 模拟试卷
- 预测试卷
1. 已知复数 

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2. 记等差数列



正确答案
170
解析
解析已在路上飞奔,马上就到!
知识点
10.对于在区间











正确答案
(0,1)中间的值
解析
解析已在路上飞奔,马上就到!
知识点
11.已知函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.集合A={ 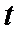
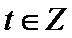
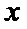
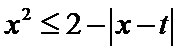
正确答案
-2
解析
解析已在路上飞奔,马上就到!
知识点
3.点


正确答案
5
解析
解析已在路上飞奔,马上就到!
知识点
4.已知曲线




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.若不等式
正确答案
2<b<4
解析
解析已在路上飞奔,马上就到!
知识点
9.已知函数


正确答案
0
解析
解析已在路上飞奔,马上就到!
知识点
5.函数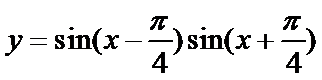
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.已知


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知命题:“非空集合

① 

② 

③ 

④ 存在

其中真命题的序号是 __________.(将正确命题的序号都填上)
正确答案
①④
解析
解析已在路上飞奔,马上就到!
知识点
18.关于



(1)求集合A;
(2)若 
正确答案
(1)A ={1,2}
(2) 

集合A={1,2}的子集有
当

解得
当B={1}或{2}时,

则m无解.
当B={1,2}时,
综上所述,实数m的取值范围是
解析
解析已在路上飞奔,马上就到!
知识点
19.如图,四棱锥



(1)棱SA的中点为M,求异面直线DM与SC所成角的大小;
(2)求侧面ASD与侧面BSC所成二面角的大小.
正确答案
(1)
(2)
解析
解析已在路上飞奔,马上就到!
知识点
20. 函数




(1)求

(2) 若



(3)若


正确答案
(1)赋值得 

(2) 



(3)设 

得
得

又
从而
解析
解析已在路上飞奔,马上就到!
知识点
17.关于x的方程 

正确答案
设实根为
则
得
得 k=5 ,
解析
解析已在路上飞奔,马上就到!
知识点
21.已知二次函数


(1) 求f (x) 的定义域D和值域 A;
(2)试用函数单调性的定义解决下列问题:
若存在实数




(3)是否存在实数t,使得A B成立?若存在,求实数t 的取值范围;若不存在,请说明理由.
正确答案
(1)定义域D =[-1,1] 值域 A=
(2)在


则
得
得
同理 由在

所以 
由
(3)由(2)的单调性分析同理可得 t 的不同取值,函数g(x)的单调性
① 当 t≤0时,函数 g(x) = x 3-3tx + 在 x∈[0,1]单调递增,∴B = [,
∴
② 当 0 < t < 1 时,函数 g(x)的减区间为:
g(x)在 x = 达到最小值。

③ 当t≥1时,函数 g(x) 在区间 [0,1]单调递减,
∴B = [
∴
综上所述:t的取值范围是:
解析
解析已在路上飞奔,马上就到!
知识点
14.设


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.若
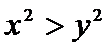
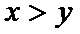
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.已知




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.若对任何

正确答案
解析
解析已在路上飞奔,马上就到!