- 真题试卷
- 模拟试卷
- 预测试卷
1.设集合


正确答案
(-1,2)
解析
解析已在路上飞奔,马上就到!
知识点
3.已知向量a=(1,2),b=(-2,-4),|c|=

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.计算: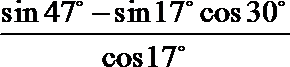
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.若命题

正确答案

解析
解析已在路上飞奔,马上就到!
知识点
7.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.等差数列




正确答案
10
解析
解析已在路上飞奔,马上就到!
知识点
2.已知

正确答案
-1
解析
解析已在路上飞奔,马上就到!
知识点
8.在数列{an}中,a1=6,且对任意大于1的正整数n,点(



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13. 函数y=3x2+
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.函数





① 
② 
③ 当

则
正确答案
1
解析
解析已在路上飞奔,马上就到!
知识点
5.已知曲线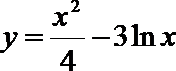

正确答案
3
解析
解析已在路上飞奔,马上就到!
知识点
12.定义在R上的函数






正确答案
(0,2)
解析
解析已在路上飞奔,马上就到!
知识点
16.





(1)求

(2)在△ABC中,




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.设函数


(1)求a、b的值;
(2)若对于任意的

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15. 已知集合A=

(1) 当

(2) 当



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.某出版社新出版一本高考复习用书,该书的成本为5元一本,经销过程中每本书需付给代理商




(1)求该出版社一年的利润L(万元)与每本书的定价
(2)若
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知数列{



(Ⅰ)令


(Ⅱ)求数列

(Ⅲ)设



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知


(1)求
(2)是否存在负实数


(3)对








正确答案
解析
解析已在路上飞奔,马上就到!




























