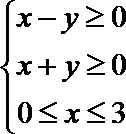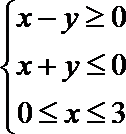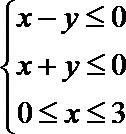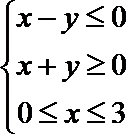- 真题试卷
- 模拟试卷
- 预测试卷
2.(1-i)2·i=( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.不等式组
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.已知集合 P = {x∈N | 1≤x≤10},集合Q = {x∈R | x2+x-6=0},则P∩Q等于( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.若函数f (x)=
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.如果

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.若动点


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.若
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4. 双曲线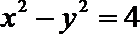
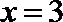
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.设



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12. 设







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.设椭圆的两个焦点分别为



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.已知


正确答案
-2
解析
解析已在路上飞奔,马上就到!
知识点
14.由动点P向圆x2+y2=1引两条切线PA、PB,切点分别为A、B,∠APB=60°,则动点P的轨迹方程为___________.
正确答案
x2+y2=4
解析
解析已在路上飞奔,马上就到!
知识点
16.已知在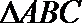
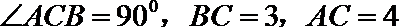
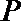
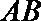
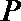
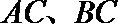
正确答案
3
解析
解析已在路上飞奔,马上就到!
知识点
15. 

正确答案
1
解析
解析已在路上飞奔,马上就到!
知识点
20.在等差数列



(Ⅰ)求数列
(Ⅱ)记



正确答案
(Ⅰ)设等差数列








(Ⅱ)由


当

当


即
解析
解析已在路上飞奔,马上就到!
知识点
21.设双曲线C:
(I)求双曲线C的离心率e的取值范围;
(II)设直线l与y轴的交点为P,且
正确答案
(I)由C与t相交于两个不同的点,故知方程组
有两个不同的实数解.消去y并整理得
(1-a2)x2+2a2x-2a2=0. ①
双曲线的离心率
(II)设
由于x1+x2都是方程①的根,且1-a2≠0,
解析
解析已在路上飞奔,马上就到!
知识点
17.如图,函数y=2sin(πx+φ),x∈R,(其中0≤φ≤
(Ⅰ)求φ的值;
(Ⅱ)设P是图象上的最高点,M、N是图象与x轴的交点,求
正确答案
(Ⅰ)因为函数图象过点(0,1)
所以 



(Ⅱ)由函数
得
所以
从而
故
解析
解析已在路上飞奔,马上就到!
知识点
18.某运动员射击一次所得环数
现进行两次射击,以该运动员两次射击中最高环数作为他的成绩,记为
(1)求该运动员两次都命中7环的概率;
(2)求
(3)求

正确答案
(1)求该运动员两次都命中7环的概率为
(2)





(3) 

解析
解析已在路上飞奔,马上就到!
知识点
19. 如图,已知四棱锥P-ABCD的底面ABCD为等腰梯形,AB∥DC,AC⊥BD,AC与BD相交于点O,且顶点P在底面上的射影恰为O点,又BO=2,PO=
(Ⅰ)求异面直接PD与BC所成角的余弦值;
(Ⅱ)求二面角P-AB-C的大小;
(Ⅲ)设点M在棱PC上,且
正确答案
解法一:


又
由平面几何知识得:
(Ⅰ)过









又




又

在
故异面直线PD与
(Ⅱ)连结






(Ⅲ)连结







故


解法二:





由平面几何知识得:

以







(Ⅰ)



故直线


(Ⅱ)设平面

由于

由
取

又二面角


(Ⅲ)设





由(1)(2)知:



故


解析
解析已在路上飞奔,马上就到!
知识点
22.已知函数
(Ⅰ)求
(Ⅱ)设





正确答案
(Ⅰ)对函数

令

当


所以,当

当

当


(Ⅱ)对函数
因此

因此当


又


任给



则
即
解

解
又
故:
解析
解析已在路上飞奔,马上就到!