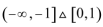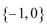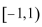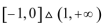- 真题试卷
- 模拟试卷
- 预测试卷
1. 已知集合



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.复数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.如图程序框图,若实数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.在极坐标系中,圆




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.若二项式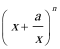
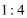
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.在等比数列



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.下图是底面半径为1,母线长均为2的圆锥和圆柱的组合体,则该组合体的体积为__________。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.从甲.乙等五人中任选三人排成一排,则甲不在排头.乙不在排尾的概率为______。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.某类产品按工艺共分10个档次,最低档次产品每件利润为8元.每提高一个档次,每件利润增加2元。 用同样工时,可以生产最低档产品60件,每提高一个档次将少生产3件产品。则获得利润最大时生产产品的档次是________。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.过点



正确答案

解析
解析已在路上飞奔,马上就到!
知识点
13.某学校随机抽取







正确答案
54
解析
解析已在路上飞奔,马上就到!
知识点
11.函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.已知全集为





① 对任意

②对任意


③对任意

④对任意

其中,正确结论的序号是__________。
正确答案
①②③
解析
解析已在路上飞奔,马上就到!
知识点
4.已知偶函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.如果函数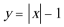
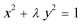
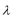
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.已知函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.设等差数列




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.如图所示,在三棱锥








(1)证明
(2)求直线

正确答案
(1)以点




则

于是
因为


(2)由(1)可得,
于是

设平面
则





设直线


则



解析
解析已在路上飞奔,马上就到!
知识点
19.在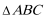
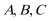
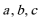
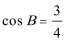
(1) 求
(2) 若
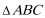
正确答案
(1)因为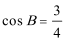
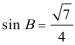
又
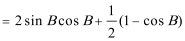
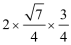
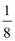
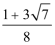
(2)由已知得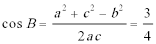
又因为
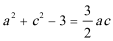
又因为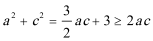
所以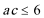
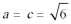
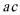
此时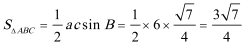
所以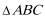
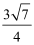
解析
解析已在路上飞奔,马上就到!
知识点
20.已知向量






(1)求函数关系式
(2)若对任意


正确答案
(1)当




当

(2)由题意知



当




当
即函数



解析
解析已在路上飞奔,马上就到!
知识点
22.已知椭圆










(1)求曲线
(2)设




(3)设






正确答案
(1)依题意可得





(2)证明:设点






则直线
联立方程组

解得
同理方程组

(3)设点



则







又


由(2)知,










当


解析
解析已在路上飞奔,马上就到!
知识点
23.实数列
(1)若

(2)令




(3)是否存在实数



正确答案
(1)

(2)由

(3)
要使


当




当




而当





解析
解析已在路上飞奔,马上就到!