- 真题试卷
- 模拟试卷
- 预测试卷
3.如下图所示的程序框图.若两次输入



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.双曲线



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知集合



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.复数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.不等式组
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6. 若锐角


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.如图是一台微波炉的操作界面.若一个两岁小孩触碰
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8. 下列命题中真命题的个数为( )
①

②锐角

③

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.二项式


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.某几何体的三视图如下所示,若该几何体的外接球的表面积为

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.平行四边形






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.已知实数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.在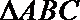
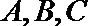
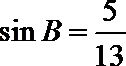
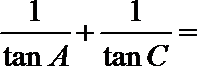
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.将正奇数





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.对于
①若

②若

③若

④若
其中正确命题的序号为_____________。
正确答案
③④
解析
解析已在路上飞奔,马上就到!
知识点
19. 已知四边形




(1)若



(2)若二面角


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17. 已知数列






(1)求数列
(2)若数列




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.某校学生会组织部分同学,用“10分制”随机调查“阳光”社区人们的幸福度.现从调查人群中随机抽取12名,如图所示的茎叶图记录了他们的幸福度分数(以小数点前的一位数字为茎,小数点后的一位数字为叶):
(1)指出这组数据的众数和中位数;
(2)若幸福度不低于9.5分,则称该人的幸福度为“极幸福”.求从这12人中随机选取3人,至多有1人是“极幸福”的概率;
(3)以这12人的样本数据来估计整个社区的总体数据,若从该社区(人数很多)任选2人,记

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21. 已知函数



(1)求实数
(2)若存在


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20. 已知椭圆C:




(1)求椭圆C的方程;
(2)AB是经过右焦点F的任一弦(不经过点P),设直线




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
选做题:请考生在22、23、24三题中任选一题作答,如果多做,则按题号最前的一题给分.
22.如图所示,
(I)求证:BD=AE
(Ⅱ)若
23.极坐标系中,已知点A,B的极坐标分别为

(Ⅰ)求曲线C的极坐标方程;
(Ⅱ)以极点为直角坐标系原点,极轴为x正半轴建立直角坐标系xoy,设点M(x,y)在曲线C上移动,求式子
24.设函数
(Ⅰ)当a=2时,求函数y=f(x)的值域;
(Ⅱ)当


22.如图所示,
(I)求证:BD=AE
(Ⅱ)若

23. 极坐标系中,已知点







(Ⅰ)求曲线
(Ⅱ)以极点为直角坐标系原点,极轴为




24.设函数

(Ⅰ)当

(Ⅱ)当