- 真题试卷
- 模拟试卷
- 预测试卷
3. 已知



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2. 函数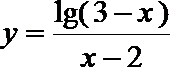
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6. 若


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4. 从
正确答案
66
解析
解析已在路上飞奔,马上就到!
知识点
5. 已知点A分有向线段


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8. 在平行四边形











正确答案
解析


知识点
11. 已知等边三角形


正确答案
1
解析
由于

则
∵
∴
知识点
1. 设集合
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7. 从0到9这10个数字中任取3个数字组成一个没有重复数字的三位数,这个数不能被3整除的概率为______________.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10. 在直角坐标系






正确答案
解析
∵ 点C在∠AOB的平分线上,
∴ 设
=

∴

∴
知识点
13. 在如图所示的数阵中,分别按图中虚线,从上到下把划到的数一一列出,构成一个数列










正确答案
21
解析
解析已在路上飞奔,马上就到!
知识点
12. 设




正确答案
18
解析
由

所以



知识点
14. 中国象棋中规定:马每走一步只能按日字格(也可以是横日“ ”)的对角线走.例如马从方格中心点O走一步,会有8种走法. 则从图中点A走到点B,最少需__________步,按最少的步数走,共有__________种走法.
正确答案
4;8
解析
解析已在路上飞奔,马上就到!
知识点
9. 已知等比数列







正确答案
121
解析
解析已在路上飞奔,马上就到!
知识点
22.对于任意的复数

(1) 集合


(2) 若

(3) 直线






正确答案
(1)
由于
得
(2)若
则
若
则




(3)
由题意:
得
所以


得
②当
得

此时
即

解析
解析已在路上飞奔,马上就到!
知识点
19.已知向量


(1)求函数
(2)若
正确答案
(1)∵


∵
(2)
解析
解析已在路上飞奔,马上就到!
知识点
21.已知



(1)当


(2)求使不等式

正确答案
(1)当



∵ 
∴
解得 

∴ 当


(2)∵ 
∴ 当

当

当

当

当

解析
解析已在路上飞奔,马上就到!
知识点
20.已知某地今年年初有居民住房的总面积为



(1)分别写出第一年末和第二年末的实际住房面积的表达式;
(2)如果第五年末该地的住房面积正好比今年年初的住房面积增加了30%,则每年拆除的旧住房面积

正确答案
(1)第1年末的住房面积:
第2年末的住房面积:
(2)第3年末的住房面积:
第4年末的住房面积:
第5年末的住房面积:
=
由题意可知,
所以每年拆除的旧房面积为
解析
解析已在路上飞奔,马上就到!
知识点
23.已知










(1)求



(2)已知







(3)在(2)的条件下,设








正确答案
(1)∵点

设
又
即
∴

①当




②当




=
综合①②得,
(2)由(1)知
当


∴
当





① +②得,
当

∴
(3)








∴


当
∴
解析
解析已在路上飞奔,马上就到!
知识点
15. 设等比数列






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16. 已知









正确答案
解析
由





同理

知识点
18. 已知向量




正确答案
解析
由




知识点
17. 如图,一质点

















正确答案
解析
探究