- 真题试卷
- 模拟试卷
- 预测试卷
4.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.设


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.设命题







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知两条直线
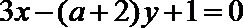
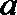
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.在等差数列





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.下列函数中,在其定义域内,既是奇函数又是减函数的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.已知函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知等差数列





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知二次函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.已知P(x,y)是直线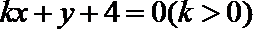
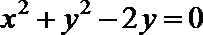
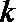
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知椭圆


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.若焦点在x轴上的椭圆


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.若不等式组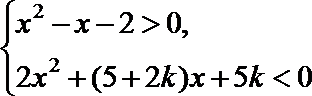
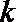
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.当实数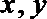
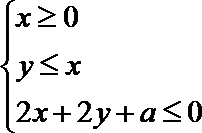
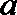
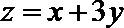
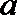
正确答案
-12
解析
解析已在路上飞奔,马上就到!
知识点
14.若直线



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.在

(1)求
(2)若
正确答案
解:(1)因为a,b,c成等差数列,所以a+c=2b,
又

所以
(2)由(1)

因为
所以
得
解析
解析已在路上飞奔,马上就到!
知识点
20.已知单调递增的等比数列



(1)求数列
(2)若


正确答案
(1)设等比数列

依题意,有
代入

又
(2)




又
当



解析
解析已在路上飞奔,马上就到!
知识点
19.设函数
(1)写出函数的最小正周期及单调递减区间;
(2)当



(3)将满足(2)的函数






正确答案
(1)
∴
由

故函数

(2)
当


(3)由题意知

解析
解析已在路上飞奔,马上就到!
知识点
18.如图,AD

(1)求证:AF∥平面BDE;
(2)求证:平面BDE
正确答案
(1)证明:∵AD⊥平面ABC,AC

∴AD⊥AC,AD⊥AB,
∵AD∥CE,∴CE⊥AC
∴四边形ACED为直角梯形.
又∵∠BAC=90°,∴AB⊥AC,∴AB⊥面ACED.
∴凸多面体ABCED的体积
求得CE=2.
取BE的中点G,连结GF,GD,
则GF∥EC,GF
∴GF∥AD,GF=AD,四边形ADGF为平行四边形,
∴AF∥DG.
又∵GD

∴AF∥平面BDE.
(2)证明:∵AB=AC,F为BC的中点,
∴AF⊥BC.
由(1)知AD⊥平面ABC,AD∥GF,∴GF⊥面ABC.
∵AF
又BC
又∵DG∥AF,∴DG⊥面BCE.
∵DG
解析
解析已在路上飞奔,马上就到!
知识点
21.已知长方形ABCD,
(1)求以A、B为焦点,且过C、D两点的椭圆的标准方程;
(2)过点P(0,2)的直线


正确答案
(1)由题意可得点A,B,C的坐标分别为
设椭圆的标准方程是
则
∴椭圆的标准方程是
(2)由题意直线的斜率存在,可设直线

设M,N两点的坐标分别为
联立方程:
消去
有
若以MN为直径的圆恰好过原点,则

所以,
即
所以,
即
得
所以直线


所在存在过P(0,2)的直线

解析
解析已在路上飞奔,马上就到!
知识点
22.已知函数


(1)若
(2)在(1)的条件下,求经过点


(3)设函数

正确答案
(1)由已知得,
由




当



又
由题意得


(2)解:由(1)得

当切点为P(2,1)时,切线



当切点P不是切点时,设切点为




又点P(2,1)在






故所求切线


(3)解:


二次函数









当

可知函数
解析
解析已在路上飞奔,马上就到!