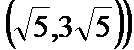- 真题试卷
- 模拟试卷
- 预测试卷
2．已知各项均为正数的等比数列{
A
B7
C6
D4
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
5．若直线 过
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
1．设全集
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
4．已知 
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
6．已知
A若
B若
C若
D若 
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
7．如果若干个函数的图象经过平移后能够重合，则称这些函数为“同簇函数”。给出下列函数：
①
②
③
④
其中“同簇函数”的是（ ）
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
8．已知某几何体的三视图如图，其中正（主）视图中半圆的半径为1，则该几何体的体积为（ ）
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
9．正六棱柱的底面边长为4，高为6，则它的外接球的表面积为（ ）
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
10．若直线
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
11．设函数
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
12．若对任意
（1）非负性：
（2）对称性：
（3）三角形不等式：
今给出四个二元函数：
①
② 
③
④
能够成为关于的
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
3．已知
A
B
C
D．
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
13．在
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
14．已知
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
15．若圆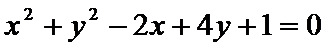
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
16．在正方形
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
18．已知锐角
（1）求
（2）若
正确答案
（1）因为
且
所以
（2）由
得
即
由①②解得
解析
解析已在路上飞奔，马上就到！
知识点
17．命题
命题
若命题“
正确答案
命题
即
命题
圆心
即
解得
由命题“
若
若
综上知实数
解析
解析已在路上飞奔，马上就到！
知识点
19．已知数列{an}的前n项和为Sn，且满足an＝
（1）求数列{an}的通项公式；
（2）若
正确答案
（1） an＝
an-1＝
①-②得：an＝2an-1（n≥2），
又易得a1＝2
∴ an＝2n
（2） bn＝n，
裂项相消可得
∵
∴ 欲
须
又k正整数，
∴ k=5、6、7
解析
解析已在路上飞奔，马上就到！
知识点
20．已知函数
（1）若函数
（2）当
正确答案
（1）由值域为
当
有
即
则
由已知
解得
不等式
∴
解得
（2）当
所以
因为
所以
令
当
当
所以当
因为
所以
所以
解析
解析已在路上飞奔，马上就到！
知识点
21．四棱锥
（1）求证：
（2）求证：
（3）求二面角
正确答案
（1）
（2） 
所以
由①②可知，
（3）取
由 （2）知
即二面角
解法二 （1）
所以
建系
因为平面PAB的法向量
（2）
（3） 设平面PAD的法向量为
令
平面PAB的法向量
即二面角
解析
解析已在路上飞奔，马上就到！
知识点
22．在实数集R上定义运算：
（1）求F（x）的解析式；
（2）若F（x）在R上是减函数，求实数a的取值范围；
（3）若a=－3，在F（x）的曲线上是否存在两点，使得过这两点的切线互相垂直？若存在，求出切线方程；若不存在，说明理由。
正确答案
（1）由题意，F（x）=f（x） 
=ex（a－e－x－2x2）
=aex－1－2x2ex．
（2）∵F′（x）=aex－2x2ex－4xex=－ex（2x2+4x－a），
当x∈R时，F（x）在减函数，
∴F′（x）≤0对于x∈R恒成立，即
－ex（2x2+4x－a）≤0恒成立，
∵ex>0，
∴2x2+4x－a≥0恒成立，
∴△=16－8（－a） ≤0，
∴a≤－2．
（3）当a=－3时，F（x）= －3ex－1－2x2ex，
设P（x1，y1），Q（x2，y2）是F（x）曲线上的任意两点，
∵F′（x）= －ex（2x2+4x+3）
=－ex[2（x+1）2+1]<0，
∴ F′（x1）·F′（x2）>0，
∴F′（x1）·F′（x2）= －1 不成立．
∴F（x）的曲线上不存在两点，使得过这两点的切线点互相垂直．
解析
解析已在路上飞奔，马上就到！