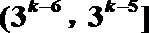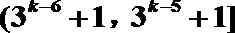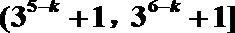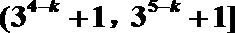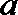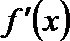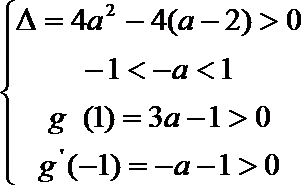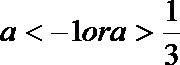- 真题试卷
- 模拟试卷
- 预测试卷
2. 下列函数中,在其定义域内既是奇函数又是减函数的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3. 等差数列








正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6. 某展览会一周(七天)内要接待三所学校学生参观。每天只安排一所学校,其中甲学校要连续参观两天,乙、丙两学校均参观一天且参观安排在甲学校参观之后,则不同的安排方法的种类( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7. 已知偶函数








正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10. 已知函数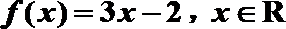
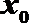
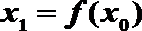
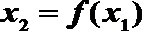
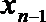
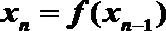
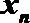
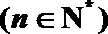
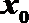
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.设全集是实数集R, M={x|x≤1+

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5. 锐角三角形




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4. 已知





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8. 设












正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.设函数








正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11. 已知



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12. 已知



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13. 已知
正确答案
3
解析
解析已在路上飞奔,马上就到!
知识点
17. 在△ABC中,


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14. 设

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.设A=






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15. 设奇函数





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知关于


(1)当

(2)对于不等式的解集





正确答案
当


当

(2) 由(1)知:当

当


因为

所以当

此时

解析
解析已在路上飞奔,马上就到!
知识点
20. 已知数列







(1)求证:数列
(2)记

(3)设数列




正确答案
(3)
∴
故当






解析
解析已在路上飞奔,马上就到!
知识点
21.已知曲线























(1)分别求

(2)设O为坐标原点,求
正确答案
解:(1)∵
∴曲线




此切线与


∴点

∵点

∴曲线


令


∴数列


解析
解析已在路上飞奔,马上就到!
知识点
22. 已知函数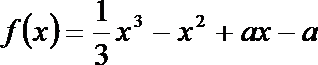
(1)当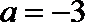
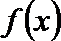
(2)设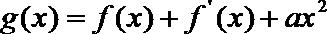
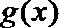
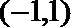
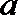
(3)若函数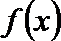
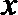
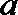
正确答案
解:(1)当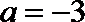
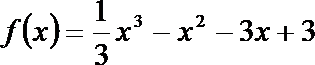
∴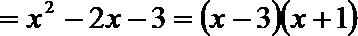
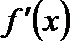
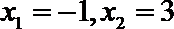
当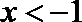
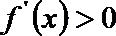
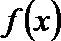
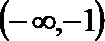
当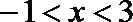
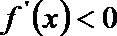
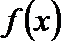
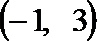
当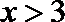
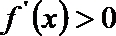
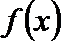
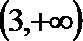
问题转化为方程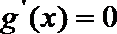
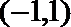
∴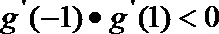
解得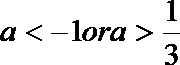
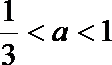
(3) ∵ 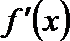
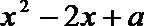
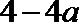
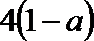
① 若a≥1,则△≤0, ∴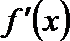
∴ f(x)在R上单调递增 .
∵f(0)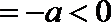
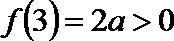
∴当a≥1时,函数f(x)的图象与x轴有且只有一个交点.
当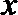
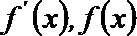
∵
∴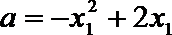
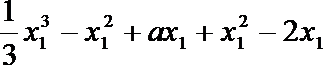
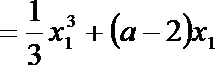
解析
解析已在路上飞奔,马上就到!
知识点
18. [已知向量



(1)求函数
(2)在







正确答案
解析
解析已在路上飞奔,马上就到!