- 真题试卷
- 模拟试卷
- 预测试卷
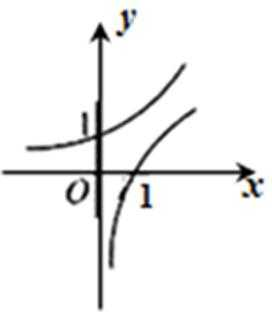
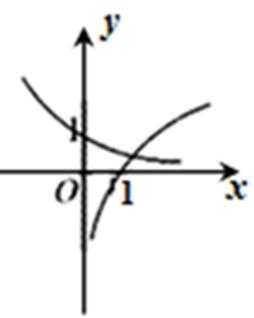
2.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知幂函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.定义集合运算:


正确答案
16
解析
解析已在路上飞奔,马上就到!
知识点
9.已知集合

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.如果



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.命题“若两个数都是正数,则它们的和是正数”的否命题为( )
正确答案
若两个数不都是正数,则它们的和不是正数
解析
解析已在路上飞奔,马上就到!
知识点
6.集合


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知


正确答案
8
解析
解析已在路上飞奔,马上就到!
知识点
10.已知命题





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.不等式


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.函数
正确答案
3
解析
解析已在路上飞奔,马上就到!
知识点
13.已知函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.设函数






①
②
③
④



正确答案
③④
解析
解析已在路上飞奔,马上就到!
知识点
17.已知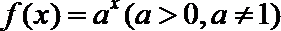
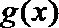
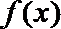
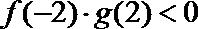
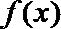
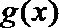
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.已知函数





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.下列命题中正确的是:( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.设集合P={x|x2=1},Q={x|ax=1},则Q

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知集合
(1)求集合
(2)若

正确答案
(1)
所以
(2)
所以
解析
解析已在路上飞奔,马上就到!
知识点
20.已知函数
(1)求实常数
(2)设




正确答案
(1)
所以,当

(2)由


当
当



所以,
解析
解析已在路上飞奔,马上就到!
知识点
22.已知函数



(1)求
(2)若不等式


(3)若

正确答案
(1)
令






由已知得
故
(2)

化为


因




所以

(3)原方程可化为









记


解不等组①,得


解析
解析已在路上飞奔,马上就到!
知识点
23.函数






(1)指出函数


(2)试研究对数函数



(3)若



①举一例说明满足条件的函数
②若对任意


③试研究:在不同条件下,函数
正确答案
(1)

(2)研究对数函数







当



当



总之,当


当


(3)①例如函数

②若对任意



当


综上讨论,当


③1)若对任意


2)若对任意











3)若存在




4)若函数

解析
解析已在路上飞奔,马上就到!
知识点
21.某商场在国庆促销期间规定:商场内所有商品按标价的80%出售;同时,当顾客在该商场内消费满一定金额后,按如下方案相应获得第二次优惠(获得奖券):
根据上述促销方法,顾客在该商场购物可以获得双重优惠。例如:购买标价为600元的商品,则消费金额为480元,480∈[400,500),所以获得第二次优惠金额为60元,获得的优惠总额为:600×0.2+60=180(元)。
设购买商品的优惠率=
试问:(1)购买一件标价为1000元的商品,顾客得到的优惠率是多少?
(2)设顾客购买标价为x元(x∈[250,1000]) 的商品获得的优惠总额为y元,试建立y关于x的函数关系式;
(3)对于标价在[625,800)(元)内的商品,顾客购买商品的标价的取值范围为多少时,可得到不小于
正确答案
(1)标价为1000元的商品消费金额为800元,获得奖券150元,优惠额为350元,所以优惠率为0.35
(2)y=
(3)购买标价在[625,800)(元)内的商品,消费金额在[500,640)(元)内。
设顾客购买标价为x元的商品,(625≤x<800),消费金额为0.8x.获得奖券100元,此时优惠率为
综上所述,顾客购买标价的取值范围为[625,750](元)时,可得到不小于
解析
解析已在路上飞奔,马上就到!