- 真题试卷
- 模拟试卷
- 预测试卷
3. 下列命题中,是真命题的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4. 已知△


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5. 若



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10. 设函数






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.复数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2. 若双曲线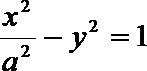
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6. 一个几何体的三视图如图所示,其中正视图和侧视图是腰长为1的等腰直角三角形,则该几何体的外接球的表面积是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7. 如图,函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8. 已知集合







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9. 设两圆

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11. 设函数


正确答案
3
解析
解析已在路上飞奔,马上就到!
知识点
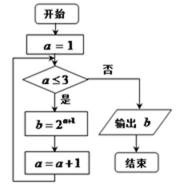
12. 如图所示的程序框图,输出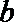
正确答案
16
解析
解析已在路上飞奔,马上就到!
知识点
14.如图,半径为1的⊙




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.设




①不论


②若


③若


④若





⑤若





正确答案
①②③
解析
解析已在路上飞奔,马上就到!
知识点
13.设等差数列




正确答案
42
解析
解析已在路上飞奔,马上就到!
知识点
20.点






(1)试判断△
(2)若△


正确答案
解:
(1)由

设


由题意知

则


所以
又由


(2)由(1)知,不妨设



由

由
由


所以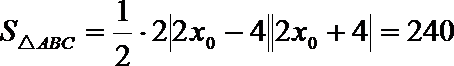
解得
若


若


解析
解析已在路上飞奔,马上就到!
知识点
16.若函数


(1)求函数
(2)若点



正确答案
解:(1)
由



因为切点的横坐标依次成公差为
所以

(2)由(1)知,令
由
所以点
解析
解析已在路上飞奔,马上就到!
知识点
17. 某地发生特大地震和海啸,使当地的自来水受到了污染,某部门对水质检测后,决定往水中投放一种药剂来净化水质.已知每投放质量为






(Ⅰ)如果投放的药剂质量为
(Ⅱ)如果投放的药剂质量为

正确答案
解:(Ⅰ)因为

当

综上
所以自来水达到有效净化一共可持续8天.
(Ⅱ)由


即
在区间

综上
为使



所以为了使在7天之内的自来水达到最佳净化,投放的药剂质量
解析
解析已在路上飞奔,马上就到!
知识点
18. 如图,已知多面体






(1)求证:

(2)求多面体
正确答案
(1)证明:由计算可
可证

∴
(2)解:可证该几何体是直三棱柱的一部分,其体积为
解析
解析已在路上飞奔,马上就到!
知识点
19.已知函数


(1)求
(2)讨论关于

正确答案
解:(1)由


从而可求得
(2)由
令

当


当


当

而
当

当


当

解析
解析已在路上飞奔,马上就到!
知识点
21.对于数列














(1)设数列








(2)设数列



①若

②若

(3)设数列











正确答案
(1)证明:

所以

所以
(2)当



当

即

①由



由于对任意的


②由



存在


即当

(3)假设存在
于是


所以


则

当

当

当

当

所以
为使


综上,假设存在


解析
解析已在路上飞奔,马上就到!