- 真题试卷
- 模拟试卷
- 预测试卷
2. 若


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.已知双曲线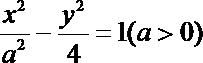
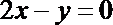
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.某市连续5天测得空气中PM2.5(直径小于或等于2.5微米的颗粒物)的数据(单位:
正确答案
31.6(写成
解析
解析已在路上飞奔,马上就到!
知识点
7.已知5瓶饮料中有且仅有2瓶是果汁类饮料。从这5瓶饮料中随机取2瓶,则所取2瓶中至少有一瓶是果汁类饮料的概率为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.若曲线
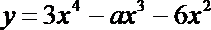

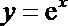

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知实数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.设集合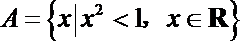
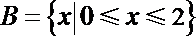
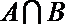
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.某学校选修羽毛球课程的学生中,高一,高二年级分别有80名,50名。现用分层抽样的方法在这130名学生中抽取一个样本,已知在高一年级学生中抽取了24 名,则在高二年级学生中应抽取的人数为( )
正确答案
15
解析
解析已在路上飞奔,马上就到!
知识点
6.函数
正确答案
π
解析
解析已在路上飞奔,马上就到!
知识点
10.给出下列命题:
(1)若两个平面平行,那么其中一个平面内的直线一定平行于另一个平面;
(2)若两个平面平行,那么垂直于其中一个平面的直线一定垂直于另一个平面;
(3)若两个平面垂直,那么垂直于其中一个平面的直线一定平行于另一个平面;
(4)若两个平面垂直,那么其中一个平面内的直线一定垂直于另一个平面。
则其中所有真命题的序号为( )
正确答案
(1)(2)
解析
解析已在路上飞奔,马上就到!
知识点
12.已知函数f(x)=

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.在平面直角坐标系





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.在△ABC中,角A,B,C的对边分别为a,b,c,若


正确答案
4
解析
解析已在路上飞奔,马上就到!
知识点
16.如图,在直三棱柱


(1)求证:EF∥平面ABC;
(2)求证:平面

(3)若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.在△ABC中,角A,B,C的对边分别为a,b,c.设向量
(1)若

(2)若


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.在平面直角坐标系






(1)求椭圆E的标准方程;
(2)如果OP是OM,OQ的等比中项,那么
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.设等差数列



(1)求数列
(2)若






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.几名大学毕业生合作开设






①当

②当


(1)求

(2)求该打印店月利润
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
22.如图,三棱锥P-ABC中,已知平面PAB⊥平面ABC,AC⊥BC,AC=BC=2a,点O,D分别是AB,PB的中点,PO⊥AB,连结CD。
(1)若
(2)若二面角A-PB-C的余弦值的大小为
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知函数
(1)当

(2)求函数
(3)当






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
23.设集合A,B是非空集合M的两个不同子集,满足:A不是B的子集,且B也不是A的子集。
(1)若M=
(2)若M=
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.【选做题】
在A、B、C、D 四小题中只能选做两题。解答时应写出文字说明、证明过程或演算步骤。
A.选修4-1:几何证明选讲
如图,等腰梯形ABCD内接于


求证:
B.选修4-2:矩阵与变换
已知直线



C.选修4-4:坐标系与参数方程
在极坐标系中,已知点


D.选修4-5:不等式选讲
已知


正确答案
A.
B.
C.
D.
解析
解析已在路上飞奔,马上就到!