- 真题试卷
- 模拟试卷
- 预测试卷
1.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.设全集

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.方程
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.不等式


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.命题 “如果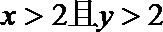
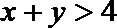
正确答案
如果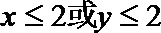
解析
解析已在路上飞奔,马上就到!
知识点
5.若


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.设




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3. 函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.在平面直角坐标系



正确答案
4
解析
解析已在路上飞奔,马上就到!
知识点
9.在平面直角坐标系





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.对实数







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知实数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.若关于



正确答案

解析
解析已在路上飞奔,马上就到!
知识点
13.函数




正确答案
(3,1)
解析
解析已在路上飞奔,马上就到!
知识点
15.已知集合


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知条件



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.设


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.对于函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知集合


(1)求
(2)若

正确答案
(1)



所以A∪B=
(2)因为

因此实数a的取值范围是
解析
解析已在路上飞奔,马上就到!
知识点
21.为了在夏季降温和冬季供暖时减少能源损耗,房屋的屋顶和外墙需要建造隔热层.某幢建筑物要建造可使用







(1)求

(2)隔热层修建多厚时,总费用
正确答案
(1)设隔热层厚度为

由

而隔热层建造费用为
最后得隔热层建造费用与
(2)

所以
(当且仅当

故

答:当隔热层修建

解析
解析已在路上飞奔,马上就到!
知识点
20.在

(1)求角
(2)求
正确答案
(1)由

得
所以
因为
又

(2)根据正弦定理得
所以

解析
解析已在路上飞奔,马上就到!
知识点
23.对于函数




(1)下面给出两组函数,

第一组:
第二组:
(2)设




(3)设








正确答案
(1)① 设

取


② 设

则


(2)


也即
因为

则
函数



(3)由题意,得



假设存在最大的常数

于是设
=
令

设

设





解析
解析已在路上飞奔,马上就到!
知识点
22.设

(1)当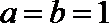

(2)设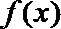


(3)当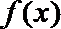
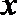

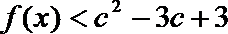
正确答案
(1)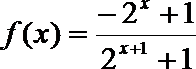

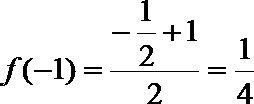
所以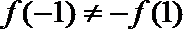
因此,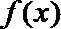
(2)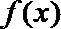
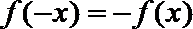
即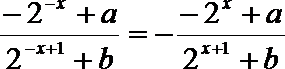
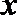
化简整理得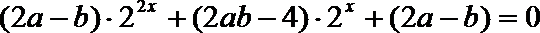
这是关于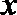

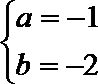
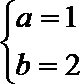
(3)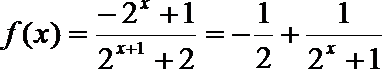
因为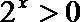
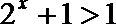
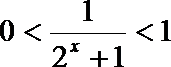

而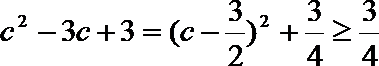
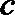
所以对任何实数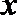
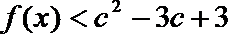
解析
解析已在路上飞奔,马上就到!