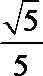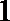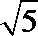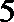- 真题试卷
- 模拟试卷
- 预测试卷
3.已知向量





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.在圆




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.将函数





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.设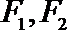


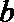

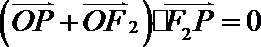
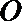

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.已知集合


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2. 已知复数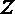
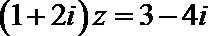
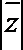
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5. 执行下边的程序框图,若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8. .设函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.已知直线




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.对于函数





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知椭圆


(1)求椭圆
(2)不过原点的直线







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.营养学家指出,高中学生良好的日常饮食应该至少提供0.075kg的碳水化合物,0.06kg的蛋白质,0.06kg的脂肪。1kg食物





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.己知函数
(1)讨论函数
(2)设




(3)求证:
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.数列


(1)若

(2)若







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.已知函数
(1)求函数
(2)记





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
选做题:请考生在第22、23、24三题中任选一题做答,如果多做,则按所做的第一题记分.
22.选修4—1:几何证明选讲
如图,在正





(1)求证:
(2)若正

23.选修4—4;坐标系与参数方程.
已知曲线




(1)写出曲线

(2)求曲线

24.选修4-5:不等式选讲
已知函数
(1)解不等式
(2)设函数

22.选修4—1:几何证明选讲
如图,在正







⑴求证:
⑵若正

23.选修4—4;坐标系与参数方程.
已知曲线







⑴写出曲线

⑵求曲线



24.选修4-5:不等式选讲
已知函数
⑴解不等式
⑵ 设函数


正确答案
正确答案
正确答案
13. 若双曲线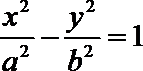
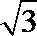
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.已知数列




正确答案
8或64
解析
解析已在路上飞奔,马上就到!
知识点
16. 已知下列四个命题:
①若


②锐角三角形


③已知



④定义在







其中的真命题是_________。
正确答案
②④
解析
解析已在路上飞奔,马上就到!
知识点
15.已知函数



正确答案
解析
解析已在路上飞奔,马上就到!