- 真题试卷
- 模拟试卷
- 预测试卷
2.集合A={0,2,a},B={1,a2},若A∪B={0,1,2,4,16},则a的值为( )
正确答案
4
解析
∵A={0,2,a},B={1,a2},A∪B={0,1,2,4,16}
∴
∴a=4
故答案为:4
知识点
4.平面直接坐标系xoy中,角α的始边与x轴的正半轴重合,终边在直线y=﹣
正确答案
±
解析
在直线y=﹣


再由sinα=


故答案为±
知识点
8.设向量



正确答案
3
解析
由向量夹角公式可得,cos120°=

∴k>0
整理可得,k2=9
∴k=3
故答案为:3
知识点
1.若复数
正确答案
-1
解析
∵


∴a+1=0且1-a≠0,
∴a=-1.
故答案为:-1
知识点
3.经过点(2,-1),且与直线2x-3y-1=0垂直的直线方程是( )
正确答案
3x+2y-4=0
解析
根据题意,易得直线2x-3y-1=0的斜率为
根据互相垂直的直线的斜率的关系,可得l的斜率为
又由直线经过点(2,-1),
则所求的直线方程为y+1=-
故答案为:3x+2y-4=0
知识点
5.某学校有两个食堂,甲、乙、丙三名学生各自随机选择其中的一个食堂用餐,则他们在同一个食堂用餐的概率为( )
正确答案
解析
甲、乙、丙三名学生选择每一个食堂的概率均为
则他们同时选中A食堂的概率为:

他们同时选中B食堂的概率也为:

故们在同一个食堂用餐的概率P=

故答案为:
知识点
6.下图是一个算法流程图,则执行该算法后输出的s=( )
正确答案
81
解析
当i=1时,不满足退出循环的条件,S=3,i=2;
当i=2时,不满足退出循环的条件,S=9,i=3;
当i=3时,不满足退出循环的条件,S=27,i=4;
当i=4时,不满足退出循环的条件,S=81,i=5;
当i=5时,满足退出循环的条件,
故答案为:81
知识点
7.设△ABC的内角A,B,C的对边分别为a,b,c,且a=1,b=2,cosC=
正确答案
解析
∵C为三角形的内角,cosC=
∴sinC=

又a=1,b=2,
∴由余弦定理c2=a2+b2﹣2abcosC得:c2=1+4﹣1=4,
解得:c=2,
又sinC=
∴由正弦定理




故答案为:
知识点
9.过点
正确答案
2x﹣4y+3=0
解析
验证知点
当∠ACB最小时,直线l与CM垂直,
由圆的方程,圆心C(1,0)
∵kCM=
∴kl=
∴l:y-1=

故应填2x-4y+3=0
知识点
10.已知函数f(x)=
正确答案
a>1或a<-
解析
当x≥0时,
所以y=log2(
此时的最大值是f(0)=log2(
当x<0时,y=(
此时的最小值(
所以函数在R上是减函数。
因为f(3-2a2)>f(a),
所以3-2a2<a,2a2+a-3>0,
解得a>1或a<-
故答案为:a>1或a<-
知识点
12.如图,在平面直角坐标系xoy中,A1,A2,B1,B2为椭圆
正确答案
解析
解法一:由题意,可得直线A2B2的方程为
两直线联立得T(

即e2+10e﹣3=0,解得
故答案为
解法二:对椭圆进行压缩变换,

椭圆变为单位圆:x'2+y'2=1,F'(
延长TO交圆O于N
易知直线A1B1斜率为1,TM=MO=ON=1,
设T(x′,y′),则
由割线定理:TB2×TA1=TM×TN


易知:B1(0,﹣1)
直线B1T方程:
令y′=0

即原椭圆的离心率e=
故答案:
知识点
14.已知f(x)=cosx,g(x)=sinx,记Sn=2

正确答案
5
解析
由题意,an=2

∴Sn=
∴Tm=S1+S2+…+Sm=2m+1﹣
∴m的最大值为5.
故答案为:5
知识点
11.设函数f(x)=



正确答案
解析
观察:f1(x)=f(x)=


可知:分子都是x,分母是关于x的一次式,其常数项为2n,一次项的系数比常数项小1,故fn(x)=
故答案为
知识点
13.已知函数f(x)=

正确答案
解析
函数f(x)=
可得函数f(x)的单调减区间为(﹣∞,﹣

单调增区间为(﹣

f(x)的极大值为f(


将直线y=m进行平移,可得当m=1时,两图象有且仅有三个不同的公共点,
相应地方程f(x)=m(m∈R)有且仅有三个不同的实数根。
令f(x)=1,得x1=




∴β•sin(




故答案为:
知识点
15.在△ABC中,角A,B,C的对边分别为a,b,c,且
(Ⅰ)求
(Ⅱ)若
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知⊙C过点P(1,1),且与⊙M:(x+2)2+(y+2)2=r2(r>0)关于直线x+y+2=0对称。
(1)求⊙C的方程;
(2)设Q为⊙C上的一个动点,求
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.设数列{an},对任意n∈N*都有(kn+b)(a1+an)+p=2(a1+a2…+an),(其中k、b、p是常数)。
(1)当k=0,b=3,p=-4时,求a1+a2+a3+…+an;
(2)当k=1,b=0,p=0时,若a3=3,a9=15,求数列{an}的通项公式;
(3)若数列{an}中任意(不同)两项之和仍是该数列中的一项,则称该数列是“封闭数列”。当k=1,b=0,p=0时,设Sn是数列{an}的前n项和,a2-a1=2,试问:是否存在这样的“封闭数列”{an},使得对任意n∈N*,都有Sn≠0,且
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.如图,2012年春节,摄影爱好者S在某公园A处,发现正前方B处有一立柱,测得立柱顶端O的仰角和立柱底部B的俯角均为30°,已知S的身高约为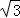
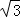
(1)求摄影者到立柱的水平距离和立柱的高度;
(2)立柱的顶端有一长2米的彩杆MN绕中点O在S与立柱所在的平面内旋转。摄影者有一视角范围为60°的镜头,在彩杆转动的任意时刻,摄影者是否都可以将彩杆全部摄入画面?说明理由。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.如图,椭圆C:

(1)求证:直线DE与直线BP的交点在椭圆C上。
(2)过点B的直线l1,l2与椭圆C分别交于R,S(不同于B点),且它们的斜率k1,k2满足k1•k2=-
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知函数
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ) 记函数y=F(x)的图象为曲线C.设点A(x1,y1),B(x2,y2)是曲线C上的不同两点,如果在曲线C上存在点M(x0,y0),使得:
①
②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”。
试问:函数f(x)是否存在“中值相依切线”,请说明理由。
正确答案
解析
解析已在路上飞奔,马上就到!