- 真题试卷
- 模拟试卷
- 预测试卷
5.如下图是向阳中学筹备2011年元旦晚会举办的选拔主持人大赛上,七位评委为某选手打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为 ( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知函教



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.下列命题中,正确的是 ( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.关于



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.下列四种说法中,错误的个数是( )
①命题“

②“命题

③“若
④
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.函数y=
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.对于函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.设集合

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.已知



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.过双曲线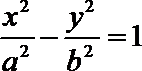
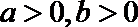
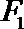
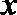
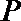
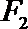
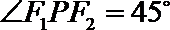
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.设m为实数,若
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.已知某程序框图如图所示,则该程序运行后输出的结果为_______。
正确答案
0.6
解析
解析已在路上飞奔,马上就到!
知识点
15.已知某实心几何体的三视图如图所示(单位:cm),则该几何体的表面积为______。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.
正确答案
14
解析
解析已在路上飞奔,马上就到!
知识点
16.已知整数对的序列如下:(1,1),(1,2),(2,1),(1,3),(2,2),(3,1),(1,4),(2,3),(3,2),(4,1),(1,5),(2,4),

正确答案
(2,12)
解析
解析已在路上飞奔,马上就到!
知识点
19.如图甲,直角梯形














(Ⅰ)求证:

(Ⅱ)当



正确答案
法一:(Ⅰ)MB//NC,MB


同理MA//平面DNC,又MA


(Ⅱ)过N作NH



DN




由MB=4,BC=2,




由条件知:
解法二:如图,以点N为坐标原点,
以NM,NC,ND所在直线分别作为


易得NC=3,MN=


(I)

∵


又

(II)设平面DBC的法向量

则




又平面NBC的法向量
即:
又

解析
解析已在路上飞奔,马上就到!
知识点
20.本着健康、低碳的生活理念,租自行车骑游的人越来越多。某自行车租车点的收费标准是每车每次租车时间不超过两小时免费,超过两小时的部分每小时收费标准为2元(不足1小时的部分按1小时计算)。有甲乙两人相互独立来该租车点租车骑游(各租一车一次),设甲、乙不超过两小时还车的概率分别为

(Ⅰ)求出甲、乙两人所付租车费用相同的概率;
(Ⅱ)设甲、乙两人所付的租车费用之和为随机变量


正确答案
解:(1)所付费用相同即为0,2,4元。设付0元为
付2元为

则所付费用相同的概率为
(2)设甲,乙两个所付的费用之和为


分布列 
解析
解析已在路上飞奔,马上就到!
知识点
18.已知等差数列


(1)求
(2)求数列

正确答案
解:(1)设等差数列

解得
所以

(2)令

所以,当



所以,当

当

所以
解析
解析已在路上飞奔,马上就到!
知识点
21.设椭圆



(I)求椭圆
(II)过点






正确答案
解:(I)由
由右焦点到直线

得:

所以椭圆C的方程为
(II)设
与椭圆






所以O到直线AB的距离 

由

即弦AB的长度的最小值是
解析
解析已在路上飞奔,马上就到!
知识点
22.设函数
(1)当

(2)当

(3)当





正确答案
解:(1)函数

当


由



故,
( 2)由题意,



若




若







②当
③当






综上,当


当


当


(3)当

∵

∴

由题意,
令



因此


所以,



∴
解析
解析已在路上飞奔,马上就到!
知识点
17.如图,某观测站C在城A的南偏西

正确答案
解:在


所以
在

所以
由正弦定理

故这时此车距离A城15千米
解析
解析已在路上飞奔,马上就到!