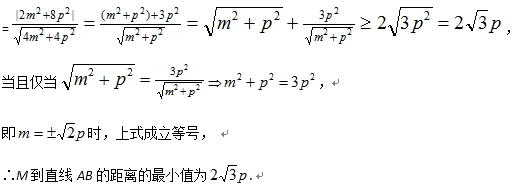- 真题试卷
- 模拟试卷
- 预测试卷
2.在等差数列

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.给出下列命题
①若直线



②若平面






③
④已知


其中正确命题的个数是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5. 在
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.若双曲线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.定义:





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.复数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.下图为一个几何体的三视图,尺寸如图所示,则该几何体的体积为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.设m,n分别是先后抛掷一枚骰子得到的点数,则在先后两次出现的点数中有5的条件下,方程
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11. 已知






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.为调查衡水市高中三年级男生的身高情况,选取了


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.如图,正方体

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知两点A (1,2), B (3,1) 到直线L的距离分别是
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13. 由直线x=
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.已知O是△ABC的外心,AB=2,AC=3,x+2y=1,若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14. 设变量x,y满足约束条件

正确答案
0
解析
解析已在路上飞奔,马上就到!
知识点
16.已知函数


下列关于
①函数
②函数
③如果当

④当

⑤函数
其中正确命题的序号____________.(写出所有正确命题的序号)
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.在

(1)求角B的大小;
(2)若

正确答案
(1)条件可化为:


由基本不等式可知
即

即当a =c=

解析
解析已在路上飞奔,马上就到!
知识点
18.如图,矩形








(Ⅰ)求证:

(Ⅱ)求二面角
正确答案
(Ⅰ)证明:因为





所以

因为


又




所以

又



所以平面

又



(Ⅱ)解:由已知平面




所以




由已知得


则




设平面

则





又


故所求二面角

解析
解析已在路上飞奔,马上就到!
知识点
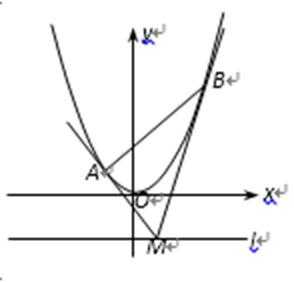
20. 如图,设抛物线方程为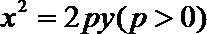
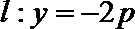
(1)设抛物线上一点P到直线l的距离为d,F为焦点,当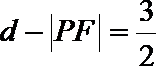
(2)求M到直线AB的距离的最小值。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.设函数f(x)=
(1)若b=-6时,函数f(x)有极大值,求实数c的取值范围;
(2)在(1)的条件下,若存在实数c,使函数f(x)在闭区间[m-2,m+2]上单调递增,求实数m的取值范围;
(3)若函数f(x)只有一个极值点,且存在t2∈(t1,t1+1),使f ′(t2)=0,证明:函数g(x)=f(x)-
正确答案
(1)因为 f(x)=
由题设,方程h(x)=0有三个互异的实根,函数h(x)=x3-12x+c,则h ′(x)=0,得x=±2.
所以
(2)存在c∈(-16,16),使f ′(x)≥0,即x3-12x≥-c,(*)所以x3-12x>-16,
即(x-2)2(x+4)>0(*)在区间[m-2,m+2]上恒成立.
所以[m-2,m+2]是不等式(*)解集的子集.
所以
(3)由题设,可得存在α,β∈R,使f ′(x)=x3+2bx+c=(x-t1)(x2+αx+β),
且x2+αx+β≥0恒成立.
又f´(t2)=0,且在x=t2两侧同号,
所以f´(x) =(x-t1)(x-t2)2.
另一方面,g ′(x)=x3+(2b-1)x+t1+c=x3+2bx+c-(x-t1)=(x-t1)[(x-t2)2-1].
因为 t1 < x < t2,且 t2-t1<1,所以-1< t1-t2 < x-t2 <0.所以 0<(x-t2)2<1,所以(x-t2)2-1<0.
而 x-t1>0,所以g ′(x)<0,所以g(x)在(t1,t2)内单调减.
从而g(x)在(t1,t2)内最多有一个零点.
解析
解析已在路上飞奔,马上就到!
知识点
从22、23、24题中任选一道作答。
22.选修4-1:几何证明选讲
自圆








试求
23.极坐标与参数方程
已知直线/经过点

(I)写出直线/的参数方程,并把圆C的方程化为直角坐标方程;
(II)设l与圆C相交于两点A、B,求点P到A、B两点的距离之积.
24.不等式选讲
已知

正确答案
22.


又



于是


23.
24.
解析
解析已在路上飞奔,马上就到!
知识点
19.某苗圃基地为了解基地内甲、乙两块地种植的同一种树苗的长势情况,从两块地各随机抽取了10株树苗,分别测出它们的高度如下(单位:cm)
甲:19 20 21 23 25 29 32 33 37 41
乙:10 26 30 30 34 37 44 46 46 47
(1)用茎叶图表示上述两组数据,并分别求两块地抽取树苗的高度的平均数和中位数;
(2)绿化部门分配这


(3)现苗圃基地将甲、乙两块地的树苗合在一起,按高度分成一、二两个等级,每个等级按不同的价格出售.某市绿化部门下属的2个单位计划购买甲、乙两地种植的树苗.已知每个单位购买每个等级树苗所需费用均为5万元,且每个单位对每个等级树苗买和不买的可能性各占一半,求该市绿化部门此次采购所需资金总额
正确答案
(1)画出茎叶图如下:
①甲地树苗高度的平均数为

②甲地树苗高度的中位数为


(2)都来自乙苗圃的概率为
(3)






∴
∴
∴该市绿化部门此次采购的资金总额
解析
解析已在路上飞奔,马上就到!