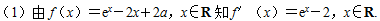- 真题试卷
- 模拟试卷
- 预测试卷
1. 已知集合A＝{2,3,4}，B＝{2,4,6,8}，C＝{（x，y）|x∈A，y∈B，且logxy∈N*}，则中元素个数是（ ）
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
2. 有四个关于三角函数的命题：
其中假命题的是 （ ）
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
4. 曲线
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
5. 已知 
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
7．设
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
9. 图中阴影部分的面积是 （ ）
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
12． 函数
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
3. {an}是等比数列，则“a1＜a2＜a3”是“数列{an}是递增数列”的（ ）
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
6. 已知a＝
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
10．已知
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
11. 已知f（x）是R上最小正周期为2的周期函数，且当0≤x＜2时，f（x）＝x3－x，则函数y＝f（x）的图象在区间[0,8]上与x轴的交点的个数为（ ）
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
8．若定义在R上的偶函数f（x）在（－∞，0）上是减函数，且
A（
B（0，
C（0，
D（2，＋∞）
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
15. 已知函数y= f （x） 的周期为2，当x
正确答案
10
解析
解析已在路上飞奔，马上就到！
知识点
13. 已知点（
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
16． 关于
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
14. 已知函数
正确答案
（－∞，2ln 2－2]
解析
解析已在路上飞奔，马上就到！
知识点
21．已知函数
（1）求曲线
（2）当
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
17．（1）设a＞0，
（2）已知奇函数f（x）的定义域为[－2,2]，且在区间[－2,0]内递减，求满足f（1－m）＋f（1－m2）＜0的实数m的取值范围。
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
18．设f（x）是定义在R上的奇函数，且对任意实数x，恒有f（x＋2）＝－f（x），当x∈[0,2]时，f（x）＝2x－x2.
（1）求证：f（x）是周期函数；
（2）当x∈[2,4]时，求f（x）的解析式；
（3）计算f（0）＋f（1）＋f（2）＋…＋f（2 011）=0.
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
19. 某上市股票在30天内每股的交易价格P（元）与时间t（天）组成有序数对（t，P），点（t，P）落在下图中的两条线段上；该股票在30天内的日交易量Q（万股）与时间t（天）的部分数据如下表所示：
（1）根据提供的图象，写出该种股票每股交易价格P（元）与时间t（天）所满足的函数关系式；
（2）根据表中数据确定日交易量Q（万股）与时间t（天）的一次函数关系式；
（3）在（2）的结论下，用y表示该股票日交易额（万元），写出y关于t的函数关系式，并求在这30天中第几天日交易额最大，最大值是多少？
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
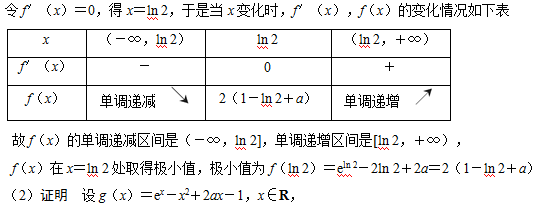
20．设a为实数，函数f（x）＝ex－2x＋2a，x∈R.
（1）求f（x）的单调区间与极值；
（2）求证：当a＞ln 2－1且x＞0时，ex＞x2－2ax＋1。
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
22. 已知函数
（1）若
（2）在函数f（x）的图像上取定点
正确答案
解析
解析已在路上飞奔，马上就到！