理科数学海淀区2013年高三试卷

精品

单选题
填空题
简答题

立即下载

理科数学热门试卷

X 查看更多试卷

试卷目录

1、单选题

2、填空题

3、简答题

真题试卷
模拟试卷
预测试卷

单选题本大题共9小题，每小题6分，共54分。在每小题给出的4个选项中，有且只有一项是符合题目要求。

题型：单选题

分值: 6分

6.函数的零点所在的一个区间是（）

A(-2，-1)

B(-1，0)

C(0，1)

D(1，2)

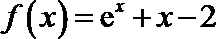
正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的加法与减法法则

题型：单选题

分值: 6分

8.根据统计，一名工人组装第x件某产品所用的时间（单位：分钟）为（A，c为常数）.已知工人组装第4件产品用时30分钟，组装第A件产品时用时15分钟，那么c和A的值分别是（）

A75，16

B75，25

C60，16

D60，25

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的运算

题型：单选题

分值: 6分

2.对于函数：

①，

②，

③，

④，

其中在区间上单调递减的函数的序号是（）

A③④

B①②

C②③

D①④

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：单选题

分值: 6分

5.设偶函数满足 (），则= （）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：单选题

分值: 6分

9.设函数的定义域为D，如果存在正实数k，使对任意，都有，且恒成立，则称函数为D上的“k阶增函数”.已知是定义在R上的奇函数，且当时，，其中为正常数.若为R上的“4阶增函数”，则实数的取值范围是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：单选题

分值: 6分

4.设函数，则满足的的取值范围是（）

A[-1，2]

B[0，2]

C[1，+

D[0，+

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：单选题

分值: 6分

7.已知函数满足：①,,②,，则（）

A是偶函数且在上单调递增

B是偶函数且在上单调递减

C是奇函数且单调递增

D是奇函数且单调递减

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：单选题

分值: 6分

1.集合 P={xZ}, M={xR}，则PM =（）

A{1,2}

B{0,1,2}

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

虚数单位i及其性质

题型：单选题

分值: 6分

3.设集合A＝{|－2＞0}，B＝{|＜0}，C＝{|}，则“A∪B”是“C”的（）

A充分而不必要条件

B必要而不充分条件

C充分必要条件

D既不充分也不必要条件

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

四种命题及真假判断

填空题本大题共7小题，每小题5分，共35分。把答案填写在题中横线上。

题型：填空题

分值: 5分

10.函数的定义域是（）．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：填空题

分值: 5分

13.三个数，由小到大的顺序是（）.

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：填空题

分值: 5分

14.已知函数，若关于的方程有两个不同的实根，则数的取值范围是（）．

正确答案

0<k<1

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：填空题

分值: 5分

15.若函数,若,则实数的取值范围是_____________.

正确答案

（-1，0）∪（1,+∞）

解析

解析已在路上飞奔，马上就到！

知识点

三角函数中的恒等变换应用

题型：填空题

分值: 5分

12.设是周期为2的奇函数,当时,,则（）．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的图像

题型：填空题

分值: 6分

16.某校数学课外小组在坐标纸上为学校的一块空地设计植树方案如下：第棵树种植在点处，其中，，当时，

表示非负实数的整数部分，例如，．按此方案，第6棵树种植点的坐标应为（）；第2008棵树种植点的坐标应为（）．

正确答案

；

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：填空题

分值: 5分

11.已知函数f(x)＝，若f(a)＋f(1)＝0，则实数a的值等于（）．

正确答案

－3

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

简答题（综合题）本大题共60分。简答应写出文字说明、证明过程或演算步骤。

题型：简答题

分值: 15分

18. 某工厂生产某种产品，每日的成本（单位：元）与日产量x（单位：吨）满足函数关系式，每日的销售额R（单位：元）与日产量x的函数关系式,已知每日的利润，且当时，.

（1）求的值；

（2）当日产量为多少吨时，每日的利润可以达到最大，并求出最大值。

正确答案

（1）由题意可得：

因为时，，所以，

所以.

（2）当

所以当时，原函数是增函数，当时，原函数是减函数

所以当时，取得最大值14300

当

所以当日产量为90吨时，每日的利润可以达到最大值14300元.

解析

解析已在路上飞奔，马上就到！

知识点

导数的乘法与除法法则

题型：简答题

分值: 15分

19.已知函数.

（1）求的最小正周期；

（2）求在区间上的取值范围.

正确答案

（1）

（2）由（1）知：

因为

所以

所以在区间上的取值范围是

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：简答题

分值: 15分

20.已知函数（）．

（1）设时，求曲线在点（处的切线方程；

（2）求的单调区间.

正确答案

（1）当

（2）

当时，

所以

故的单调递增区间是，单调递减区间是.（9分）

所以，在区间和上，，

故的单调递增区间是,单调递减区间是

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：简答题

分值: 15分

17. 已知数列是公差不为零的等差数列，，且是的等比中项.

（1）求数列的通项公式；

（2）设为数列的前项和，求使成立的所有的值。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

由数列的前几项求通项

理科数学 热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

理科数学热门试卷