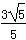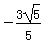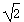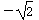- 真题试卷
- 模拟试卷
- 预测试卷
10. 设数列{





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8. 把一副三角板ABC与ABD摆成如图所示的直二面角D-AB-C,
则异面直线DC与AB所成角的正切值为 ( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2. 设全集U是实数集R,M={x|

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3. 在直角三角形ABC中,AB=4,AC=2,M是斜边BC的中点,则向量在向量方向上的投影是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7. 2位男生和3位女生共5位同学站成一排.若男生甲不站两端,3位女生中有且只有两位女生相邻,则不同排法的种数为 ( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1. 如果复数(m2+i)(1+mi)是实数,则实数m=( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4. 函数f(x)=-(cosx)|lg|x||的部分图象是 ( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9. 函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6. 已知函数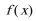
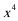
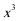
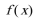
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14. 已知点


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11. 若命题“∃x∈R,使得
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12. 设


正确答案
60
解析
解析已在路上飞奔,马上就到!
知识点
13. 若下框图所给的程序运行结果为S=28,那么判断框中应填入的关于
正确答案
k≥8
解析
解析已在路上飞奔,马上就到!
知识点
15. 正方体


且 
①
②MN//平面
③MN与
④点


⑤若点




其中有可能成立的结论为____________________。
正确答案
①②④④⑤
解析
解析已在路上飞奔,马上就到!
知识点
20.已知椭圆C:+=1(a>b>0)的离心率为,短轴一个端点到右焦点的距离为。
(1)求椭圆C的方程;
(2)设直线l与椭圆C交于A、B两点,坐标原点O到直线l的距离为,求△AOB面积的最大值。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数

(1)设



(2)证明: 当

(3)设



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.如图,正方形ABCD、ABEF的边长都是1,而且平面ABCD、ABEF互相垂直,点M在AC上移动,点N在BF上移动,若CM=BN=a(0<a<
(1)求MN的长;
(2)a为何值时,MN的长最小;
(3)当MN的长最小时,求面MNA与面MNB所成二面角α的大小.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.设数列





(1)求
(2)若数列







(3)设数列




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.在

(1)求
(2) 若

(3)若函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.将10个白小球中的3个染成红色,3个染成黄色,试解决下列问题:
(1)求取出3个小球中红球个数
(2)求取出3个小球中红球个数多于白球个数的概率。
正确答案
解析
解析已在路上飞奔,马上就到!