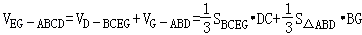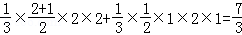- 真题试卷
- 模拟试卷
- 预测试卷
7.一个四棱锥的底面为正方形,其三视图如图所示,则这个四棱锥的体积是( )
正确答案
解析
略
知识点
8.函数y=ax(a>0,a≠1)与y=xb的图象如图,则下列不等式一定成立的是( )
正确答案
解析
略
知识点
2.集合M={1,2},N={3,4,5},P={x|x=a+b,a∈M,b∈N},则集合P的元素个数为( )
正确答案
解析
略
知识点
4.为了调查学生每天零花钱的数量(钱数取整数元),以便引导学生树立正确的消费观.样本容量1000的频率分布直方图如图所示,则样本数据落在[6,14)内的频数为( )
正确答案
解析
略
知识点
6.设x,y满足约束条件
正确答案
解析
略
知识点
1.如果复数
正确答案
解析
略
知识点
3.函数y=ln(
正确答案
解析
略
知识点
5.由曲线y=
正确答案
解析
略
知识点
9.斜率为

正确答案
解析
略
知识点
10.若一系列的函数解析式相同,值域相同但定义域不同,则称这些函数为“孪生函数”.那么函数解析式为y=2x2+1,值域为{3,19}的“孪生函数”共有( )
正确答案
解析
略
知识点
11.执行如图中的程序框,如果输入的t∈[﹣1,3],则输出的S属于区间 .
正确答案
[﹣3,4]
解析
略
知识点
13.已知命题p:函数
正确答案
(﹣∞,﹣2]∪[2,+∞)
解析
略
知识点
15.对于函数f(x),若存在常数a≠0,使得x取定义域内的每一个值,都有f(x)=﹣f(2a﹣x),则称f(x)为准奇函数.给定下列函数:
①f(x)=
②f(x)=(x﹣1)2
③f(x)=x3
④f(x)=cosx
其中所有准奇函数的序号是 .
正确答案
①④
解析
略
知识点
14.已知



正确答案
解析
略
知识点
12.若二项式
正确答案
9
解析
略
知识点
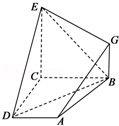
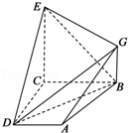
17.如图,已知四边形ABCD和BCEG均为直角梯形,AD∥BC,CE∥BG,且∠BCD=∠BCE=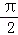
(1)EC⊥CD;
(2)求证:AG∥平面BDE;
(3)求:几何体EG﹣ABCD的体积.
正确答案
见解析。
解析
(1)证明:由平面ABCD⊥平面BCEG,
平面ABCD∩平面BCEG=BC,CE⊥BC,CE⊂平面BCEG,
∴EC⊥平面ABCD,
又CD⊂平面BCDA,故EC⊥CD
(2)证明:在平面BCEG中,过G作GN⊥CE交BE于M,连DM,
则由已知知;MG=MN,MN∥BC∥DA,且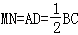
∴MG∥AD,MG=AD,故四边形ADMG为平行四边形,∴AG∥DM
∵DM⊂平面BDE,AG⊄平面BDE,∴AG∥平面BDE
(3)解:
=
知识点
18.某种产品的质量以其质量指标值衡量,质量指标值越大表明质量越好,且质量指标值大于或等于102的产品为优质品,现用两种新配方(分别称为A配方和B配方)做试验,各生产了100件这种产品,并测量了每件产品的质量指标值,得到下面试验结果:
A配方的频数分布表
B配方的频数分布表
(1)分别估计用A配方,B配方生产的产品的优质品率;
(2)已知用B配方生成的一件产品的利润y(单位:元)与其质量指标值t的关系式为y=
从用B配方生产的产品中任取一件,其利润记为X(单位:元),求X的分布列及数学期望.(以试验结果中质量指标值落入各组的频率作为一件产品的质量指标值落入相应组的概率)
正确答案
见解析。
解析
(1)由试验结果知,用A配方生产的产品中优质的频率为
∴用A配方生产的产品的优质品率的估计值为0.3.
由试验结果知,用B配方生产的产品中优质品的频率为
∴用B配方生产的产品的优质品率的估计值为0.42;
(2)用B配方生产的100件产品中,其质量指标值落入区间
[90,94),[94,102),[102,110]的频率分别为0.04,0.54,0.42,
∴P(X=﹣2)=0.04,P(X=2)=0.54,P(X=4)=0.42,
即X的分布列为
∴X的数学期望值EX=﹣2×0.04+2×0.54+4×0.42=2.68
知识点
16.已知函数f(x)=2sinxcosx+2
(1)求函数f(x)的最小正周期和单调递增区间;
(2)在锐角三角形ABC中,若f(A)=1,
正确答案
见解析。
解析
(1)f(x)=2sinxcosx+
=sin2x+
=2sin(2x+
∴函数f(x)的最小正周期为π,
由2kπ﹣


得
∴函数f(x)的单调增区间是[k

(2)由已知,f(A)=2sin(2A+
∴sin(2A+

∵0<A<

∴2A+


又∵

∴
∴△ABC的面积S=


知识点
19.已知函数f(x)=logkx(k为常数,k>0且k≠1),且数列{f(an)}是首项为4,公差为2的等差数列.
(1)求证:数列{an}是等比数列;
(2)若bn=an•f(an),当
(3)若cn=anlgan,问是否存在实数k,使得{cn}中的每一项恒小于它后面的项?若存在,求出k的范围;若不存在,说明理由.
正确答案
见解析。
解析
(1)证明:由题意f(an)=4+(n﹣1)×2=2n+2,即logkan=2n+2,
∴an=k2n+2∴
∵常数k>0且k≠1,∴k2为非零常数,
∴数列{an}是以k4为首项,k2为公比的等比数列.
(2)解:由(1)知,bn=anf(an)=k2n+2•(2n+2),
当
∴Sn=2•23+3•24+4•25+…+(n+1)•2n+2,①2Sn=2•24+3•25+…+n•2n+2+(n+1)•2n+3.②
②﹣①,得Sn=﹣2•23﹣24﹣25﹣﹣2n+2+(n+1)•2n+3=﹣23﹣(23+24+25+…+2n+2)+(n+1)•2n+3
∴
(3)解:由(1)知,cn=anlgan=(2n+2)•k2n+2lgk,要使cn<cn+1对一切n∈N*成立,
即(n+1)lgk<(n+2)•k2•lgk对一切n∈N*成立.
①当k>1时,lgk>0,n+1<(n+2)k2对一切n∈N*恒成立;
②当0<k<1时,lgk<0,n+1>(n+2)k2对一切n∈N*恒成立,只需
∵
∴当n=1时,
∴
∴
综上所述,存在实数
知识点
20.已知函数f(x)=

(1)判断函数f(x)的单调性;
(2)当m<﹣2时,求函数F(x)=f(x)+g(x)在区间[﹣2,2]上的最值;
(3)设函数h(x)=
正确答案
见解析。
解析
(1)依题意,
①当m>0时,
解f′(x)≥0得﹣2≤x≤2,解f′(x)<0得x<﹣2或x>2;
所以f(x)在[﹣2,2]上单调递增,在(﹣∞,﹣2),(2,+∞)上单调递减;
②当m<0时,
解f′(x)≤0得﹣2≤x≤2,f′(x)>0得x<﹣2或x>2;
所以f(x)在[﹣2,2]上单调递减;在(﹣∞,﹣2),(2,+∞)上单调递增.
(2)当m<﹣2,﹣2≤x≤2时,

由(1)知,f(x)在[﹣2,2]上单调递减,
所以
∴

(3)当m≥2,x1∈[2,+∞)时,

由(1)知h(x1)在[2,+∞)上单调递减,
从而h(x1)∈(0,f(2)],
即
当m≥2,x2<2时,

从而h(x2)∈(0,g(2)),即
对于任意的x1∈[2,+∞),总存在唯一的x2∈(﹣∞,2),使得h(x1)=h(x2)成立,
只需

记函数
易知
所以m的取值范围为[2,4).
知识点
21.如图,已知点S(﹣2,0)和圆O:x2+y2=4,ST是圆O的直经,从左到右M和N依次是ST的四等分点,P(异于S、T)是圆O上的动点,PD⊥ST,交ST于D,
(1)求λ的值及点C的轨迹曲线E的方程;
(2)设n是过原点的直线,l是与n垂直相交于Q点、与 轨迹E相交于A,B两点的直线,

正确答案
见解析。
解析
(1)易得T(2,0),M(﹣1,0),N(1,0),设P(x0,y0),C(x,y),则
直线PS与TE交于C,故x≠±2,

①②相乘得
又点P是圆O上的动点,故

要使|CM|+|CN|为定值,则4﹣

此时
即λ=

(2)设A,B两点的坐标分别为(x1,y1),(x2,y2),假设使
(ⅰ)当l不垂直于x轴时,设l的方程为y=kx+m,
由l与n垂直相交于Q点且|

∵

∴
即x1x2+y1y2=0,
将y=kx+m代入椭圆方程,得(3+4k2)x2+8kmx+(4m2﹣12)=0
由求根公式可得

0=x1x2+y1y2=x1x2+(kx1+m)(kx2+m)=
=
将④,⑤代入上式并化简得 (1+k2)(4m2﹣12)﹣8k2m2+m2(3+4k2)=0⑥
将m2=1+k2代入⑥并化简得﹣5(k2+1)=0,矛盾,即此时直线l不存在
(ⅱ)当l垂直于x轴时,满足
当x=1时,A,B,Q的坐标分别为
∴
∴
当x=﹣1时,同理可得
综上可知,使