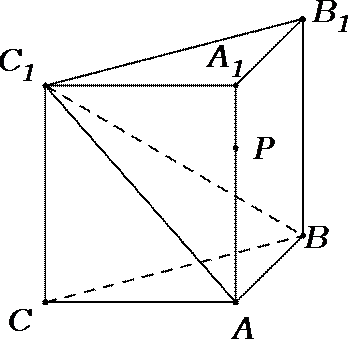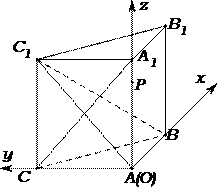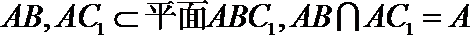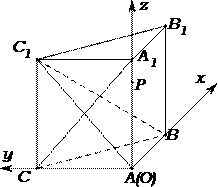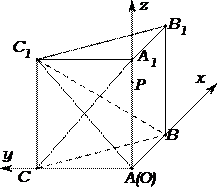- 真题试卷
- 模拟试卷
- 预测试卷
4. 执行下侧框图所表达的算法,如果最后输出的


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1. 复数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5. 下列四个条件:
①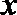
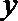
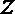
②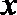
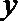
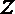
③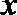
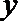
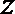
④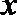

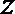
其中,能使命题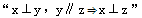
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9. 为调查某校学生喜欢数学课的人数比例,采用如下调查方法:
(1)在该校中随机抽取100名学生,并编号为1,2,3,……,100;
(2)在箱内放置两个白球和三个红球,让抽取的100名学生分别从箱中随机摸出一球,记住其颜色并放回;
(3)请下列两类学生举手:
(ⅰ)摸到白球且号数为偶数的学生;
(ⅱ)摸到红球且不喜欢数学课的学生.
如果总共有26名学生举手,那么用概率与统计的知识估计,该校学生中喜欢数学课的人数比例大约是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3. 已知

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7. 已知二次函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8. 已知






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2. 已知集合


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6. 已知实数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10. 函数的图象与方程的曲线有着密切的联系,如把抛物线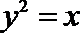
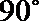
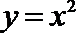
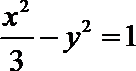
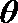
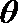
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12. 一个三棱锥的正视图和侧视图及其尺寸如图所示,则该三棱锥俯视图的面积为________.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13. 在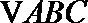
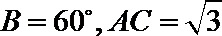
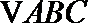
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14. 已知




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11. 已知等差数列



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15. 数学与文学之间存在着许多奇妙的联系. 诗中有回文诗,如:“云边月影沙边雁,水外天光山外树”,倒过来读,便是“树外山光天外水,雁边沙影月边云”,其意境和韵味读来真是一种享受!数学中也有回文数,如:88,454,7337,43534等都是回文数,无论从左往右读,还是从右往左读,都是同一个数,称这样的数为“回文数”,读起来还真有趣!
二位的回文数有11,22,33,44,55,66,77,88,99,共9个;
三位的回文数有101,111,121,131,…,969,979,989,999,共90个;
四位的回文数有1001,1111,1221,…,9669,9779,9889,9999,共90个;
由此推测:10位的回文数总共有________个.
正确答案
90000
解析
解析已在路上飞奔,马上就到!
知识点
18. 已知

(Ⅰ)如果该同学10所高校的考试都参加,试求恰有2所通过的概率;
(Ⅱ)假设该同学参加每所高校考试所需的费用均为


正确答案
(Ⅰ)因为该同学通过各校考试的概率均为

(Ⅱ)设该同学共参加了


∵
∴所以该同学参加考试所需费用
所以
令
则
由(1)-(2)得
所以
所以

解析
解析已在路上飞奔,马上就到!
知识点
19.如图,侧棱垂直底面的三棱柱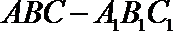
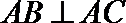
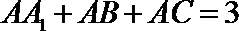
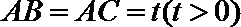
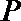
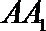
(Ⅰ)当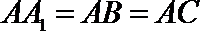
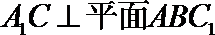
(Ⅱ)试求三棱锥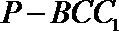
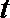
(Ⅲ)若二面角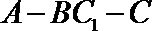
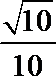
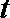
正确答案
(Ⅰ)证法一:∵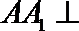
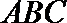
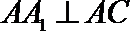
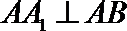
又∵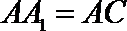
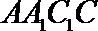
∴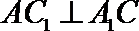
∵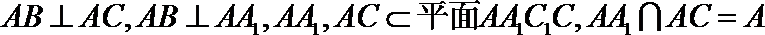
∴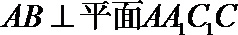
又∵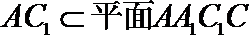
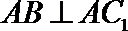
∵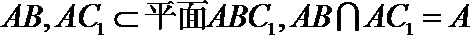
∴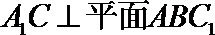
证法二:
∵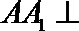
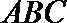
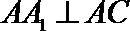
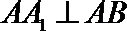
又∵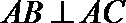
∴分别以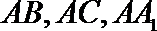
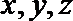
则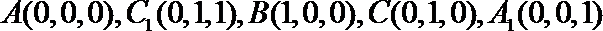
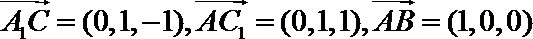
∴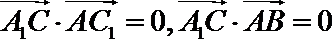
∴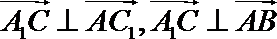
又∵
∴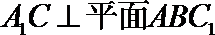
证法三:
∵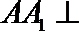
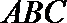
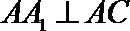
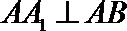
又∵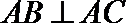
∴分别以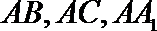
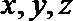
则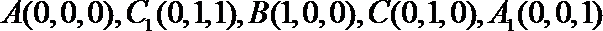
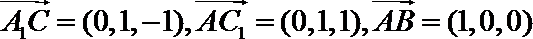
设平面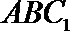
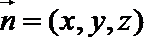
则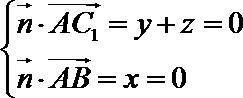
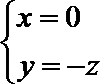
令
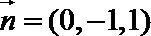
∵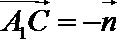
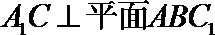
(Ⅱ)∵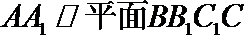
∴点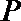
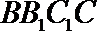
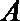
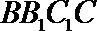
∴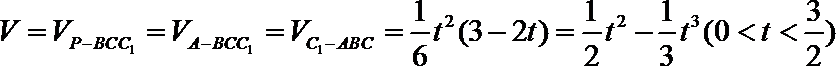
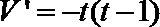
令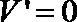
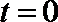
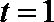
得
∴当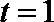
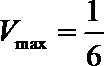
(Ⅲ)
分别以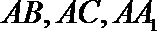
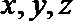
则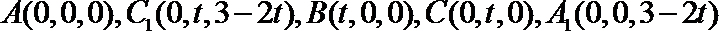
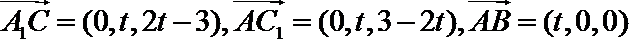
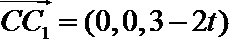
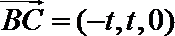
设平面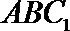
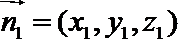
则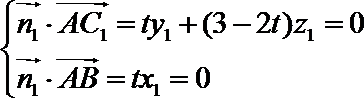
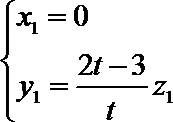
令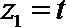
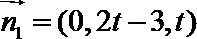
设平面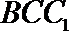
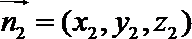
则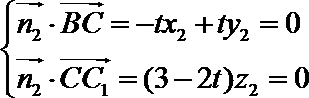
由于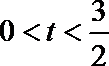
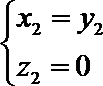
令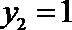
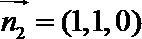
设二面角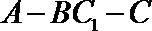
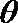
则有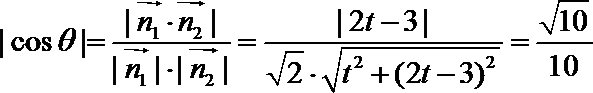
化简得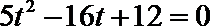
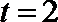
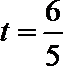
所以当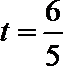
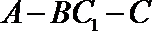
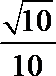
解析
解析已在路上飞奔,马上就到!
知识点
17.将边长为1的正三角形




(Ⅰ)试用


(Ⅱ)定义:对于直角坐标平面内的任意两点






正确答案
(Ⅰ)解法一:因为

所以

解法二:平移





由


由平几知识易得直线

∵

所以
(Ⅱ)解法一:
∵

∴

所以当


解法二:
∵


∴
∵

∴


所以当


解析
解析已在路上飞奔,马上就到!
知识点
16.已知点




(Ⅰ)试判断点

(Ⅱ)是否存在过




正确答案
(Ⅰ)因点


所以点




(Ⅱ)解法一:假设存在满足题设的直线



依题意,得
①当直线
②当直线


联立方程组
消去

∴

此时,方程(*)为
∴存在满足题设的直线
且直线


解法二:假设存在满足题设的直线



依题意,得
易判断直线

∴设直线

联立方程组
消去

∵
∴直线与轨迹
又

∴存在满足题设的直线
且直线


解法三:假设存在满足题设的直线



依题意,得
∵

∴有


当


∴


注意到点



∴存在满足题设的直线
且直线


解析
解析已在路上飞奔,马上就到!
知识点
20.已知




(Ⅰ)请写出
(Ⅱ)设


(Ⅲ)设





正确答案
(Ⅰ)

(Ⅱ)∵
∴当



∴当


即

(Ⅲ) 解法一:∵
又
∴
令

∵


∵

∴存在

∵

∴当



即


∴
又∵


∴当


解法二: ∵
又
∴
令
则
当




所以

又

∴当


解析
解析已在路上飞奔,马上就到!
知识点
21.本题有(1)、(2)、(3)三个选答题,请考生任选2题作答。
(1)选修4—2:矩阵与变换
若二阶矩阵

(Ⅰ)求二阶矩阵
(Ⅱ)把矩阵

(2)选修4-4:坐标系与参数方程
已知在直角坐标系








(Ⅰ)求曲线C的普通方程并说明曲线的形状;
(Ⅱ)是否存在实数





(3)选修4—5:不等式选讲
已知函数



(Ⅰ)求
(Ⅱ)求证:
正确答案
(1)选修4—2:矩阵与变换
(Ⅰ)记矩阵


由已知得
(Ⅱ)设二阶矩阵


解得
又



(2)选修4—4:坐标系与参数方程
(Ⅰ)∵

①当
②当
(Ⅱ)直线

联立直线与曲线的方程,消


若直线

又
故

解得

故不存在满足题意的实数
(3)选修4—5;不等式选讲
(Ⅰ)法一: 
可得函数的最小值为2.故
法二:
当且仅当

(Ⅱ)
即:
故
解析
解析已在路上飞奔,马上就到!