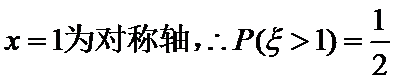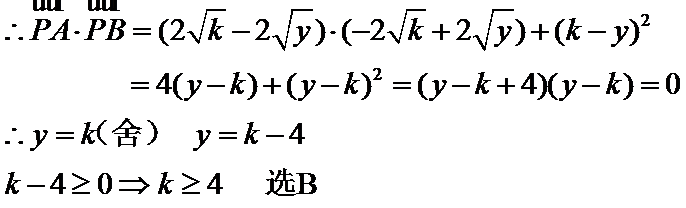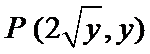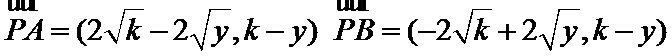- 真题试卷
- 模拟试卷
- 预测试卷
2.已知数据



正确答案
解析
数据增加一个联系实际可知500超出体重,所以平均数会增加,50个数据的中位数可能为中间第25,26两个数(数值相等),所以增加一个最大数后,中位数变为第26个,不发生变化,所以选B
考查方向
解题思路
【解题思路】本题属于简单题,可使用直接法,
易错点
数据结合实际,忽视中位数的定义
知识点
3.设随机变量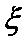
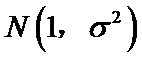
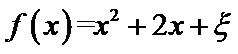
正确答案
解析
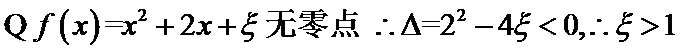
考查方向
解题思路
【解题思路】本题属于简单题,可使用直接法,
易错点
该题容易忽视正态分布曲线的对称性
知识点
9.如图,四棱锥



正确答案
解析
考查方向
易错点
本题容易在没有发现B,D点的位置关系,导致无法解答
知识点
1.已知全集

正确答案
解析
使用集合交集的性质,借助数轴容易得出答案B。
考查方向
解题思路
本题属于简单题,可使用venn图直接观察得出
易错点
直接观察漏解
知识点
4.已知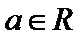
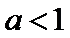
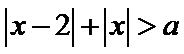
正确答案
解析
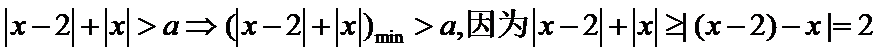
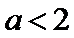
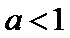
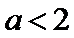
考查方向
解题思路
【解题思路】本题属于简单题,可使用直接法,
易错点
该题容易把恒成立问题的转换求错,对充分、必要条件的判定不熟导致选错
知识点
5.定义


正确答案
解析
根据题意可知
所以
考查方向
解题思路
【解题思路】本题借助于数形结合思想,
易错点
该题出错在分段不清,定积分不能有效分段
知识点
6.已知点


正确答案
解析
根据题意作图
容易得到
由双曲线的几何性质

考查方向
解题思路
【解题思路】本题属于基础题型,使用数形结合,
易错点
该题不易发现使用几何性质,导致运算变大,运算出错
知识点
7.如图所示的程序框图,输出S的值为
正确答案
解析
考查方向
解题思路
1写出循环结构,找出S结果的规律2找出程序框图解决的问题:求数列前n项和,找出首项和公比3、找出跳出循环的位置即项数
易错点
本题易在判断上出错,导致提前或者延后跳出循环,第二没有发现S结果之间的规律,导致出错,
知识点
8.已知


正确答案
解析
方法1:线性规划问题中最优解出现在可行域的顶点上,因为有三个约束条件,所以顶点即三条直线的交点(两两结合解方程组)A(1,1), B(-2,2), C(-2,-2),依次带入判断出答案C,
该方法缺点是只能解决三条直线的问题,超过三条需要判断那些点是在可行域上
方法2:画出可行域如图当直线过C(-2,-2)点时取得最优解6,选C
考查方向
解题思路
该题有两个解法,方法一:线性规划问题中最优解出现在可行域的顶点上,因为有三个约束条件,所以顶点即三条直线的交点,一一求解验证
方法二,根据条件画出可行域,平移直线
易错点
主要体现在两个方面①可行域不规范,②直线平移过程忽略直线的斜率
知识点
10.已知抛物线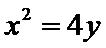
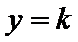
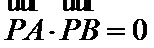
正确答案
解析
抛物线与直线y=k联立确定AB两点的坐标
设动点
则
考查方向
解题思路
本题属于多知识迁移题,需要对知识进行有效转换
(1)确定AB两点的坐标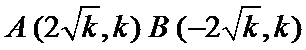
(2)向量
(3)利用向量的数量积运算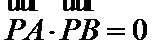
易错点
该题主要易错于题意理解错误,不能有效进行知识的转换
知识点
已知函数




16.求函数
17.在





正确答案
见解析
解析
考查方向
解题思路
该题解题思路如下1、利用倍角公式

易错点
该题易于忽略
正确答案
见解析
解析
考查方向
解题思路
该题解题思路如下1、利用倍角公式

易错点
该题易于忽略
为迎接2022年北京冬奥会,推广滑雪运动,某滑雪场开展滑雪促销活动.该滑雪场的收费标准是:滑雪时间不超过1小时免费,超过1小时的部分每小时收费标准为40元(不足1小时的部分按1小时计算).有甲、乙两人相互独立地来该滑雪场运动,设甲、乙不超过1小时离开的概率分别为

18.求甲、乙两人所付滑雪费用相同的概率;
19.设甲、乙两人所付的滑雪费用之和为随机变量



正确答案
见解析
解析
考查方向
解题思路
本题的解题思路
1、首先分清清零的所有可能,以及每种情况发生的可能。
2、分清
3、根据情况依次求概率
4、写分布列以及期望
易错点
本题第一问在情况分析上容易遗漏,第二问可能取值考虑不全
正确答案
见解析
解析
考查方向
解题思路
本题的解题思路
1、首先分清清零的所有可能,以及每种情况发生的可能。
2、分清
3、根据情况依次求概率
4、写分布列以及期望
易错点
本题第一问在情况分析上容易遗漏,第二问可能取值考虑不全
22.求数列

23.求数列

正确答案
见解析
解析
考查方向
解题思路
1、借助n=1求出

2、利用

易错点
本题第一问得不出
正确答案
见解析
解析
考查方向
解题思路
1、借助n=1求出

2、利用

易错点
本题第一问得不出
如图,在四棱锥



20.设面


21.求二面角
正确答案
见解析
解析
考查方向
解题思路
该题解题关键在于找到所求内容的突破点
1、确定线面平行判定的方式:线//面→线//线
2、由已知推出AB//CD得到线//面
3、根据线//面推导线//线
4、根据已知条件建立坐标系,并标记所需点的坐标
5、计算相应面的法向量,并求向量的夹角6、判断两面角的大小确定二面角
易错点
本题容易在辅助线建立过程出错,空间直角坐标系建立及其坐标表示出错,二面角的判断出错
正确答案
见解析
解析
考查方向
解题思路
该题解题关键在于找到所求内容的突破点
1、确定线面平行判定的方式:线//面→线//线
2、由已知推出AB//CD得到线//面
3、根据线//面推导线//线
4、根据已知条件建立坐标系,并标记所需点的坐标
5、计算相应面的法向量,并求向量的夹角6、判断两面角的大小确定二面角
易错点
本题容易在辅助线建立过程出错,空间直角坐标系建立及其坐标表示出错,二面角的判断出错
已知椭圆


24.若

25.试问:直线PQ是否过定点?若过定点,求出定点坐标;若不
正确答案
见解析
解析
考查方向
解题思路
1、根据直线BH斜率求出直线AM的斜率,并确定直线AH
2、直线AM与椭圆联立得出点P
3、假设PQ的坐标,根据AP求出点M,利用点MBQ三点共线,确定使用斜率相等,得出x1 x2的关系式
4、设直线PQ的直线方程,与曲线联立使用韦达定理确定x1 x2的关系式,带入得到m,K的关系,进而确定定点
易错点
本题主要有以下几个错误:1、抛物线焦点求措,2、无法确确定定值,进而无法确定解题过程,3、求△ABQ面积无法确定底和高
正确答案
见解析
解析
考查方向
解题思路
1、根据直线BH斜率求出直线AM的斜率,并确定直线AH
2、直线AM与椭圆联立得出点P
3、假设PQ的坐标,根据AP求出点M,利用点MBQ三点共线,确定使用斜率相等,得出x1 x2的关系式
4、设直线PQ的直线方程,与曲线联立使用韦达定理确定x1 x2的关系式,带入得到m,K的关系,进而确定定点
易错点
本题主要有以下几个错误:1、抛物线焦点求措,2、无法确确定定值,进而无法确定解题过程,3、求△ABQ面积无法确定底和高
已知函数
26.对于

27.当


28.求证:
正确答案
见解析
解析
考查方向
解题思路
本题解题思路1、第一问借助函数的换元思想,求新函数

易错点
本题易错在恒成立问题的转化不清,函数分类讨论不清,
正确答案
见解析
解析
A
考查方向
解题思路
本题解题思路1、第一问借助函数的换元思想,求新函数

易错点
本题易错在恒成立问题的转化不清,函数分类讨论不清,
正确答案
见解析
解析
考查方向
解题思路
本题解题思路1、第一问借助函数的换元思想,求新函数

易错点
本题易错在恒成立问题的转化不清,函数分类讨论不清,
12.在二项式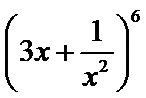
正确答案
1215
解析
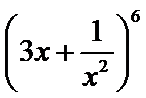
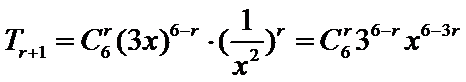
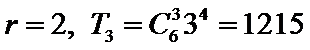
考查方向
解题思路
写出二项展开式,确定r,直接计算
易错点
本题易错在二项展开式记忆错误
知识点
15.定义在区间










正确答案
解析
由题意可知
∴
又因为
∴
所以
考查方向
解题思路
1、根据题意给定区间,把



易错点
本题易错于因为信息量大,数据处理不全,找不到解题思路
知识点
11.已知i是虚数单位,


正确答案
i
解析

考查方向
解题思路
本题属于简单题,可使用直接法,(1)根据复数相等的充要条件,求出

易错点
计算过程易忽略
知识点
13.已知函数





正确答案
解析
由题意可知
又∵函数为偶函数 ∴
又∵
考查方向
解题思路
根据正弦型函数的图像容易得到




易错点
本题易于在求解
知识点
14.若

正确答案
解析
考查方向
易错点
本题易错于使用双重不等式忽略等号成立条件