- 真题试卷
- 模拟试卷
- 预测试卷
4.下图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.函数y=loga(x+3)-1(a>0,且a≠1)的图象恒过定点A,若点A在直线mx+ny+1=0上(其中m,n>0),则
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.在△ABC中,AB=3,AC=5,若O为△ABC的外心,则
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.复数(2+i)i的虚部是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.命题“
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知变量x,y满足

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知f(x)是定义在R上的函数,f(1)=10,且对于任意x∈R都有f(x+20)≥f(x)+20,f(x+1)≤f(x)+1,若g(x)=f(x)+1-x,则g(10)=( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.某程序的框图如图所示,则执行该程序,输出的结果a=_______.
正确答案
127
解析
解析已在路上飞奔,马上就到!
知识点
10.在区间[0,1]上任取两实数a,b,则使a+b≥1的概率为_____.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.过抛物线y2=4x的焦点F作斜率为

正确答案
4
解析
解析已在路上飞奔,马上就到!
知识点
11.已知曲线y=3x2+2x在点(1,5)处的切线与直线2ax-y-6=0平行,则a=_____.
正确答案
4
解析
解析已在路上飞奔,马上就到!
知识点
选做题:14~16题,考生只能从中选做两题
14.(坐标系与参数方程)
在极坐标系中,定点A(2,π),动点B在直线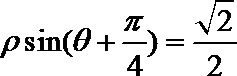
15.(几何证明选讲)
如图,在半径为2的⊙O中,∠AOB=90°,D为OB的中点,AD的延长线交⊙O于点E,则线段DE的长为____________.
16.(优选法选讲)
用0.618法选取试点的过程中,如果实验区间为[2,4],前两个试点依次为x1,x2,若x1处的实验结果好,则第三试点的值为__________.
正确答案
14.
15. 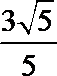
16. 3.528或2.472(填一个即可)
解析
解析已在路上飞奔,马上就到!
知识点
13.如图所示,将数以斜线作如下分群:(1),(2,3),(4,6,5),(8,12,10,7),(16,24,20,14,9),…,并顺次称其为第1群,第2群,第3群,第4群,…,
(1)第7群中的第2项是:_____;
(2)第n群中n个数的和是:_____.
正确答案
(1)96
(2)3·2n-2n-3
解析
解析已在路上飞奔,马上就到!
知识点
18.某工厂2011年第一季度生产的A,B,C,D四种型号的产品产量用条形图表示如图,现用分层抽样的方法从中选取50件样品,参加四月份的一个展销会.
(1)问A,B,C,D型号的产品各抽取多少件?从50件样品中随机的抽取2件,求这两件产品恰好是不同型号的产品的概率;
(2)从A,C型号的产品中随机的抽取3件,用ξ表示抽取A种型号的产品件数,求ξ的分布列和数学期望.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,2AC=AA1=BC=2.
(1)若D为AA1中点,求证:平面B1CD⊥平面B1C1D;
(2)当AD的长等于多少时?二面角B1-DC-C1的大小为60°.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
22.已知f(x)=lnx-ax2-bx.
(1)若a=-1,函数f(x)在其定义域内是增函数,求b的取值范围;
(2)当a=1,b=-1时,证明函数f(x)只有一个零点;
(3)f(x)的图象与x轴交于A(x1,0),B(x2,0)( x1<x2)两点,AB中点为C(x0,0),求证:f ′(x0)<0.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.已知a=(sinx,-cosx),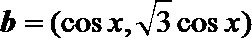
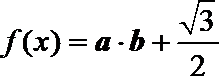
(1)求f(x)的最小正周期;
(2)当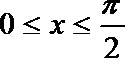
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知椭圆的中心在坐标原点O,焦点在x轴上,短轴长为2,且两个焦点和短轴的两个端点恰为一个正方形的顶点,过右焦点F与x轴不垂直的直线l交椭圆于P,Q两点.
(1)求椭圆的方程;
(2)在线段OF上是否存在点M(m,0),使得以MP,MQ为邻边的平行四边形是菱形?若存在,求出m的取值范围;若不存在,请说明理由.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.为了加强环保建设,提高社会效益和经济效益,长沙市计划用若干时间更换一万辆燃油型公交车,每更换一辆新车,则淘汰一辆旧车,替换车为电力型和混合动力型车.今年初投入了电力型公交车128辆,混合动力型公交车400辆;计划以后电力型车每年的投入量比上一年增加50%,混合动力型车每年比上一年多投入a辆.
(1)求经过n年,该市被更换的公交车总数S(n);
(2)若该市计划7年内完成全部更换,求a的最小值.
正确答案
解析
解析已在路上飞奔,马上就到!