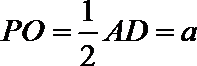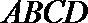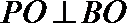- 真题试卷
- 模拟试卷
- 预测试卷
4. 

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.若点


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.已知向量



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知等比数列



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知集合

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.计算:
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.已知圆C过点




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.将标号为




正确答案
18
解析
解析已在路上飞奔,马上就到!
知识点
11.已知空间中两点



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.已知






①
②

③数列
④数列
其中正确结论的序号有_____________.
正确答案
① ③ ④
解析
解析已在路上飞奔,马上就到!
知识点
13.如图,半径为










正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.某迷宫有三个通道,进入迷宫的每个人都要经过一个智能门,首次到达此门,系统会随机(即等可能)为你打开一个通道.若是1号通道,则需要1小时走出迷宫;若是2号、3号通道,则分别需要



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.曲线




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.已知函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.记实数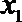
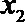
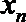
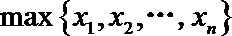
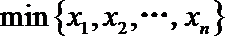
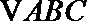
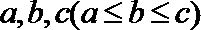
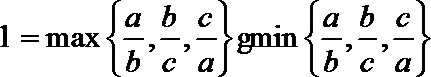
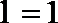
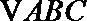
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.过正方体





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
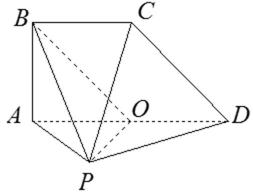
19.如图,面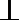
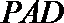
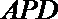
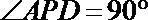
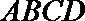
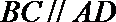
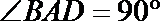
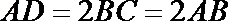
(1)求证: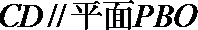
(2)求直线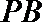
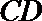
正确答案
(1)因为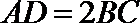
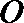
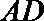
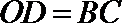
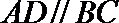
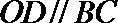
所以四边形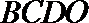
所以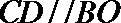
又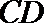
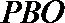
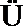
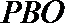
故
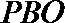
(2)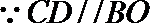
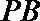
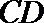
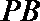
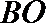
设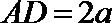
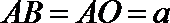
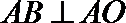
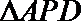
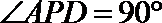
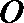
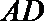
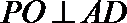
又平面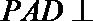
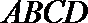
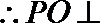
在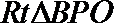
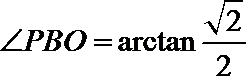
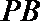
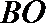
解析
解析已在路上飞奔,马上就到!
知识点
21.已知圆










(1)若

(2)求证:经过
正确答案
(1)设


解得:



(2)设




所以经过


故其方程为:
化简得:

故




解析
解析已在路上飞奔,马上就到!
知识点
20.设



(1)求角
(2)若

正确答案
(1)因为

即
所以

(2)因为

所以


解析
解析已在路上飞奔,马上就到!
知识点
22.已知数列




(1)求数列
(2)用反证法证明:数列
(3)若从数列


正确答案
(1)当


又





(2)反证法:假设存在三项按原来顺序成等差数列,记为
则2·
所以2·



(3)设抽取的等比数列首项为


则







将

经验证得

综上可得满足题意的等比数列有两个.
解析
解析已在路上飞奔,马上就到!
知识点
23.已知函数
(1)若

(2)当方程

(3)若对于一切


正确答案
(1)由
当

当




所以不等式
(2)由
令
由函数图像知两函数图像在y轴右边只有一个交点时满足题意

由
(3)
当


所以
当
①当


令


所以


所以
所以
②当

即
所以
综上,
解析
解析已在路上飞奔,马上就到!