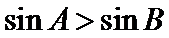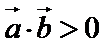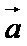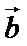理科数学海口市2012年高三试卷

精品

单选题
填空题
简答题

立即下载

理科数学热门试卷

X 查看更多试卷

试卷目录

1、单选题

2、填空题

3、简答题

真题试卷
模拟试卷
预测试卷

单选题本大题共12小题，每小题5分，共60分。在每小题给出的4个选项中，有且只有一项是符合题目要求。

题型：单选题

分值: 5分

2. 某流程如图所示，现输入如下四个函数，则可以输出的函数是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的乘法与除法法则

题型：单选题

分值: 5分

4. 设，若是纯虚数，则的关系一定是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的乘法与除法法则

题型：单选题

分值: 5分

8. 若函数，则函数的最大值是（）

A11

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

题型：单选题

分值: 5分

7. 下列判断错误的是（）

A一个命题的否命题为真，则它的逆命题一定为真

B回归直线过样本点的中心

C中，“”是“”的充要条件

D设为非零向量，若，则与的夹角为锐角

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

求函数y＝Asin(ωx＋φ)的解析式

题型：单选题

分值: 5分

9. 从男女共有36名的大学生中任选2名去考“村官”，任何人都有同样的当选机会，若选出的同性大学生的概率为，则男女生相差（）名

D10

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

复合函数的单调性

题型：单选题

分值: 5分

10. 若集合，且，则集合构成的图形的面积为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

幂函数图象及其与指数的关系

题型：单选题

分值: 5分

6. 已知是两个不共线的向量，它们的起点相同，且三个向量的终点在同一直线上，则的值是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的乘法与除法法则

题型：单选题

分值: 5分

1. 由于方程的曲线呈“心”的形状，因此，人们称之为“爱心方程式”.此“爱心方程式”所表示的曲线关于（）对称

A轴

B轴

C直线

D原点

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的乘法与除法法则

题型：单选题

分值: 5分

3. 已知命题：“若，，则”成立，那么字母在空间所表示的几何图形不能（）

A都是直线

B都是平面

C是直线，是平面

D是平面，是直线

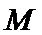
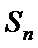
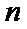
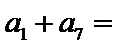
正确答案

解析

解析已在路上飞奔，马上就到！

知识点

直线与平面平行的判定与性质

题型：单选题

分值: 5分

5. 已知数列满足，则等于（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

幂函数图象及其与指数的关系

题型：单选题

分值: 5分

11. 已知向量，曲线上的一点到的距离为11，是的中点，则（为坐标原点）的值为（）

D或

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的乘法与除法法则

题型：单选题

分值: 5分

12. 已知，函数在上为增函数的概率是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的乘法与除法法则

填空题本大题共4小题，每小题5分，共20分。把答案填写在题中横线上。

题型：填空题

分值: 5分

14. 记是数列的前项和，且，则_________

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

求函数y＝Asin(ωx＋φ)的解析式

题型：填空题

分值: 5分

15. 二项式的展开式中存在常数项，则正整数的最小值是______

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

排列、组合及简单计数问题

题型：填空题

分值: 5分

16. 以“爱心曲线”在轴的交点、为椭圆的焦点，且椭圆经过曲线上到原点的最大距离对应的点，则椭圆的离心率为______

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

指数函数的图像变换

题型：填空题

分值: 5分

13. 已知一个几何体的三视图均是边长为1的正方形，那么该几何体外接球的表面积为__________

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

对数函数的定义

简答题（综合题）本大题共70分。简答应写出文字说明、证明过程或演算步骤。

题型：简答题

分值: 12分

19. 某橡胶加工厂生产甲、乙两种产品，每种产品都是经过第一和第二道工序加工而成.两道工序的加工结果相互独立，每道工序的加工结果均有、两个等级.已知加工出的甲、乙产品为级的概率分别为、，且每一件产品的利润如表一

（1）用、分别表示一件甲、乙产品的利润，求、的分布列及、；

（2）又已知生产一件产品需用的工人数和资金额如表二，该橡胶加工厂有工人40名，可用资金600元，设、分别表示生产甲、乙产品的工人数量，问当、分别为何值时，最大？最大值是多少？

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的加法与减法法则

题型：简答题

分值: 12分

20. 函数称为逻辑斯蒂克函数，此函数也是动物或昆虫繁衍的数学模型.今有

（1）求函数在上的最值；

（2）在函数图像的所有切线中，是否存在切线与直线垂直？请说明你的理由.

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

求函数y＝Asin(ωx＋φ)的解析式

题型：简答题

分值: 12分

17. 在三棱锥中，是的中点，，其余棱长均为2.

（1）求证：平面平面；

（2）求二面角的平面角的正切值。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

直线、平面垂直的综合应用

题型：简答题

分值: 12分

18. 已知函数，若成等比数列

（1）求的值；

（2）试探求函数的性质。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的乘法与除法法则

题型：简答题

分值: 12分

21. 已知圆内一点，点在圆上运动.若的垂直平分线交于一点

（1）求点的轨迹方程；

（2）在点的轨迹上是否存在关于点对称的两点？若存在，请求出对称点的坐标；若不存在，请说明理由.

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

指数函数的图像变换

题型：简答题

分值: 10分

选做题：请考生在第22、23、24题中任选一题做答，如果多做，则按所做的第一题记分.

22.（选修4-1几何证明选讲）

如图，、都是圆的切线长，，是圆的割线，交圆于

（1）求证：；

（2）延长交于F，求证：四点共圆.

23.（选修4-4坐标系与参数方程）

以平面直角坐标系的原点为极点，x轴的正半轴为极轴建立极坐标系.

（1）试分别将曲线的极坐标方程和曲线的参数方程（为参数）化为直角坐标方程和普通方程；

（2）若红蚂蚁和黑蚂蚁分别在曲线和曲线上爬行，求红蚂蚁和黑蚂蚁之间的最大距离（视蚂蚁为点）.

24.（选修4-5不等式选讲）

已知函数的定义域为

（1）求函数的定义域；

（2）若对，都有，求证：。

22.（选修4-1几何证明选讲）如图，、都是圆的切线长，，是圆的割线，交圆于，

（1）求证：；

（2）延长交于，求证：四点共圆.

23.（选修4-4坐标系与参数方程）以平面直角坐标系的原点为极点，轴的正半轴为极轴建立极坐标系.

（1）试分别将曲线的极坐标方程和曲线的参数方程（为参数）化为直角坐标方程和普通方程；

（2）若红蚂蚁和黑蚂蚁分别在曲线和曲线上爬行，求红蚂蚁和黑蚂蚁之间的最大距离（视蚂蚁为点）.

第(1)小题正确答案及相关解析

正确答案

22. （选修4-5不等式选讲）已知函数的定义域为.

（1）求函数的定义域；

（2）若对，都有，求证：.

第(2)小题正确答案及相关解析

理科数学 热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

正确答案

理科数学热门试卷