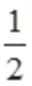理科数学黄浦区2014年高三试卷

精品

填空题
单选题
简答题

立即下载

理科数学热门试卷

X 查看更多试卷

试卷目录

1、填空题

2、单选题

3、简答题

真题试卷
模拟试卷
预测试卷

填空题本大题共14小题，每小题4分，共56分。把答案填写在题中横线上。

题型：填空题

分值: 4分

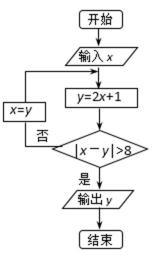
3．执行如下图所示的程序框图，若输入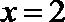，则输出的值为__________．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

程序框图

题型：填空题

分值: 4分

4．若的展开式中只有第六项的二项式系数最大，则展开式中的常数项是__________

正确答案

180

解析

解析已在路上飞奔，马上就到！

知识点

复合函数的单调性

题型：填空题

分值: 4分

7．已知，则的值为__________

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

指数函数的单调性与特殊点

题型：填空题

分值: 4分

10．正项等比数列中，存在两项使得，且，则最小值__________

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的乘法与除法法则

题型：填空题

分值: 4分

1．已知，其中是实数，是虚数单位，则的共轭复数为__________

正确答案

2-i

解析

解析已在路上飞奔，马上就到！

知识点

指数函数的图像变换

题型：填空题

分值: 4分

2．已知线性方程组的增广矩阵为，若该线性方程组解为，则实数__________．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

指数函数的图像变换

题型：填空题

分值: 4分

6．中心在原点，焦点在x轴上的双曲线的一条渐近线为，焦点到渐近线的距离为3，则该双曲线的方程为______

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

二次函数的应用

题型：填空题

分值: 4分

8．已知，，则__________

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

简单复合函数的导数

题型：填空题

分值: 4分

9．有一个正四面体的棱长为，现用一张圆形的包装纸将其完全包住（不能裁剪纸，但可以折叠），那么包装纸的最小半径为__________．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

指数函数的图像变换

题型：填空题

分值: 4分

11．已知曲线的极坐标方程分别为，，则曲线与交点的极坐标为__________．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

题型：填空题

分值: 4分

12．若为内一点，且，在内随机撒一颗豆子，则此豆子落在内的概率为__________

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

题型：填空题

分值: 4分

14．已知函数是偶函数，且，当时，，则方程在区间上的解的个数是__________

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

二次函数的应用

题型：填空题

分值: 4分

13．如图，矩形的一边在轴上，另外两个顶点在函数的图象上．若点的坐标为，记矩形的周长为，则__________

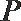
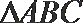
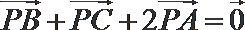
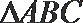
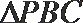
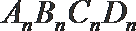
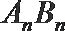
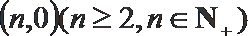
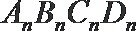
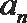
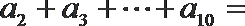
正确答案

216

解析

解析已在路上飞奔，马上就到！

知识点

简单复合函数的导数

题型：填空题

分值: 4分

5．已知集合，，且，则__________

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

交集及其运算绝对值不等式的解法

单选题本大题共4小题，每小题5分，共20分。在每小题给出的4个选项中，有且只有一项是符合题目要求。

题型：单选题

分值: 5分

17．圆的圆心到直线（为参数）的距离为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

题型：单选题

分值: 5分

15．若为空间两条不同的直线，，为空间两个不同的平面，则丄的一个充分条件是（）

A//且丄

B且丄

C丄且//

D丄且//

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

复合函数的单调性

题型：单选题

分值: 5分

16．某中学高二年级的一个研究性学习小组拟完成下列两项调查：

①从某社区430户高收入家庭，980户中等收入家庭，290户低收入家庭中任意选出170户调查社会购买力的某项指标；

②从本年级12名体育特长生中随机选出5人调查其学习负担情况；则该研究性学习小组宜采用的抽样方法分别是（）

A①用系统抽样，②用随机抽样

B①用系统抽样，②用分层抽样

C①用分层抽样，②用系统抽样

D①用分层抽样，②用随机抽样

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

题型：单选题

分值: 5分

18．若函数的图象如下图1，其中为常数．则函数的大致图象是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

指数函数的图像变换

简答题（综合题）本大题共74分。简答应写出文字说明、证明过程或演算步骤。

题型：简答题

分值: 14分

20．如图，某市准备在道路EF的一侧修建一条运动比赛道，赛道的前一部分为曲线段FBC．该曲线段是函数时的图象，且图象的最高点为，赛道的中间部分为长千米的直线跑道CD，且//；赛道的后一部分是以O为圆心的一段圆弧．

（Ⅰ）求的值和的大小；

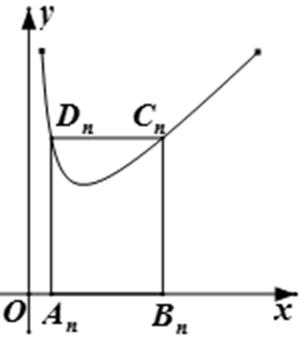
（Ⅱ）若要在圆弧赛道所对应的扇形ODE区域内建一个“矩形草坪”，矩形的一边在道路EF上，一个顶点在半径OD上，另外一个顶点P在圆弧上，求“矩形草坪”面积的最大值，并求此时点的位置．

正确答案

（Ⅰ）由条件，得，．

∵ ，∴．

∴ 曲线段FBC的解析式为．

当x=0时，．又CD=，

∴ ．

（Ⅱ）由（Ⅰ）知．

当“矩形草坪”的面积最大时，

点P 在弧DE上，故．

设，，“矩形草坪”的面积为

=．

∵ ，

故取得最大值．

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：简答题

分值: 14分

21．已知函数

（1）求函数的定义域；

（2）若，试比较的大小；

（3）设，若函数有且只有一个零点，求实数k的取值范围．

正确答案

（1）

（2）在上递减，所以“”

（3）

解析

解析已在路上飞奔，马上就到！

知识点

简单复合函数的导数

题型：简答题

分值: 12分

19．如图，为矩形，为梯形，平面平面，，．

（Ⅰ）若为中点，求证：∥平面；

（Ⅱ）求平面与所成锐二面角的大小．

正确答案

（Ⅰ）证明：连结，交与，连结，

在中，分别为两腰的中点，

∴ ，

面，又面，

平面，

（Ⅱ）解法一：设平面与所成锐二面角的大小为，

以为空间坐标系的原点，分别以所在直线

为轴建立空间直角坐标系，

则

设平面的单位法向量为，

则可设

设面的法向量，应有

，

即：，

解得：，

所以，

∴ ，

所以平面与所成锐二面角为60°．

解析

解析已在路上飞奔，马上就到！

知识点

直线与平面平行的判定与性质

题型：简答题

分值: 16分

22．已知椭圆C：的短轴的端点分别为A，B（如图），直线AM，BM分别与椭圆C交于E，F两点，其中点M （m，）满足，且．

（1）用m表示点E，F的坐标；

（2）证明直线EF与y轴交点的位置与m无关．

（3）若∆BME面积是∆AMF面积的5倍，求m的值．

正确答案

（1），M （m，），且，

直线AM的斜率为k1=，直线BM斜率为k2=，

直线AM的方程为y= ，

直线BM的方程为y= ，

由得，

；

（2）据已知，，

直线EF的斜率

直线EF的方程为，

令x=0，得

EF与y轴交点的位置与m无关．

（3），

，，

，

整理方程得，

即，

又，，

，

为所求．

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的图像

题型：简答题

分值: 18分

23．设数列对任意都有（其中、、是常数）．

（I）当，，时，求；

（II）当，，时，若，，求数列的通项公式；

（III）若数列中任意（不同）两项之和仍是该数列中的一项，则称该数列是“封闭数列”．当，，时，设是数列的前项和，，试问：是否存在这样的“封闭数列” ，使得对任意，都有，且．若存在，求数列的首项的所有取值；若不存在，说明理由．

正确答案

（I）当，，时，

， ①

用去代得，

，②

②—①得，，，

在①中令得，，则0，

∴，

∴数列是以首项为1，公比为3的等比数列，

∴=

（II）当，，时，

，③

用去代得，

，④

④—③得，，⑤．

用去代得，

，⑥

⑥—⑤得，，

即，．

∴数列是等差数列．

∵，，

∴公差，

∴

（III）由（II）知数列是等差数列，

∵，∴．

又是“封闭数列”，

得：对任意，必存在使

，

得，故是偶数，

又由已知，，故．

一方面，当时，

，对任意，

都有．

另一方面，

当时，，，

则，

取，则，不合题意．

当时，，

，则

，

当时，

，，

，

又，

∴或或或

解析

解析已在路上飞奔，马上就到！

知识点

指数函数的单调性与特殊点

理科数学 热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

理科数学热门试卷