- 真题试卷
- 模拟试卷
- 预测试卷
6. 将函数f(x)=2sin



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.复数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7. 如图,在△ABC中,AD=2DB,AE=3EC,CD与BE交于F,
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.给出如下四个命题:
①若“



②命题“若



③“

④在△


其中不正确的命题的个数是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3. 点






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4. 已知直线

①α∥β
②α⊥β
③l∥m 
④l⊥m
其中正确命题的序号是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.符号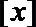
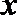
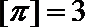
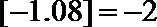

①函数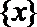
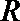
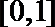
②方程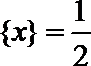
③函数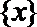
④函数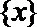
其中正确命题的序号有( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
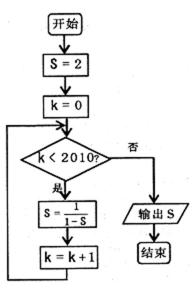
5.如果执行如图的程序框图,那么输出的值是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9. 已知函数





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10. 当


正确答案
k≤1
解析
解析已在路上飞奔,马上就到!
知识点
13.下列给出的四个命题中:
①已知数列{an},那么对任意的n∈N.,点Pn(n,an)都在直线y=2x+l上是{an}为等差数列的充分不必要条件;
②“m=-2”是“直线(m+2)x+my+1=0与直线(m-2)x+(m+2)y-3=0相互垂直”的必要不充分条件;
③设圆x2+y2+Dx+Ey+f=0与坐标轴有4个交点,分别为A(xl,0),B(x2,0),C(0,y1).D(0,
④在实数数列{an}中,已知al=0,| a2 |=| a1-l|,|a3 |=| a2-l|,…,| an |=| an-1-1|,则al+a2+a3+a4的最大值为2.
其中为真命题的是__________(写出所有真命题的代号).
正确答案
①③④
解析
解析已在路上飞奔,马上就到!
知识点
12.从四棱锥S—ABCD的八条棱中任取两条,其中抽到两条棱成异面直线的概率为__________.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11. 设



正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
14~15题是选做题,只能选做一题,两题全答的,只计算前一题得分.
14.在极坐标系中,直线



15.如图所示,已知PC、DA为⊙O的切线,C、A分别为切点,AB为⊙O的直径,若DA=2,=,则AB=________.
正确答案
14.
15. 4
解析
解析已在路上飞奔,马上就到!
知识点
19.若椭圆





(Ⅰ)求过(

(Ⅱ)设过原点的一条射线
①若P是线段AB上的一点,若|OA|、|OP|、|OB|成等比数列,求P点的轨迹方程;
②求
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21. 已知数列


(1)求数列
(2)数列



(3)设




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.某种家用电器每台的销售利润与该电器的无故障时间T(单位:年)有关,若T







(Ⅰ)求
(Ⅱ)记

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.设函数f(x)=



(1)求ω的值;
(2)如果f(x)在区间

(3)证明:直线5x-2y+c=0与函数y=f(x)的图象不相切.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.如图,四边形









(1)求证:
(2)求二面角
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.设函数
(Ⅰ)当

(Ⅱ)当

(Ⅲ)当





正确答案
解析
解析已在路上飞奔,马上就到!