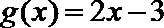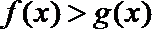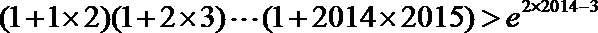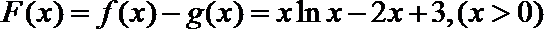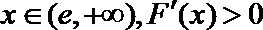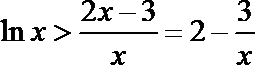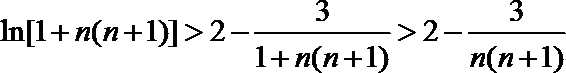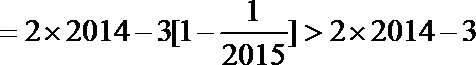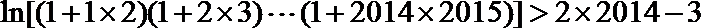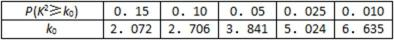- 真题试卷
- 模拟试卷
- 预测试卷
3.设x,y∈R,向量a=(x,1),b=(1,y),c=(2,-4),且a⊥c,b∥c,则=( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.如图是一个几何体的三视图,正视图和侧视图均为矩形,俯视图中曲线部分为半圆,尺寸如图,则该几何体的全面积为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知直线l1:4x-3y+6=0和直线l2:x=-1,抛物线y2=4x上一动点P到直线l1和直线l2的距离之和的最小值是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11. 设







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1. 设集合

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.复数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.设
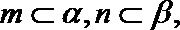
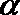
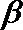
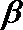
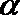

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.如图,正方形街道





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.小白散步后不慎走丢了,家里很着急,小新和阿呆等6人分配到A,B,C三条街道中寻找,每条街道至少安排1人,其中小新和阿呆同组,且小新不能分配到A街道,则不同的分配方案有( )种。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.执行如图所示的程序框图,输出的S值为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.若函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.有两个等差数列



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.在面积为S的矩形ABCD内随机取一点P,则△PBC的面积小于
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
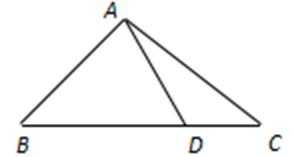
14.如图, 在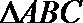
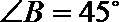
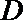
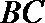
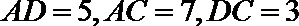
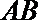
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.在平面直角坐标系中,若不等式组(a为常数)所表示的平面区域的面积等于2,则a的值为_____________。
正确答案
3
解析
解析已在路上飞奔,马上就到!
知识点
17. 已知数列








(1)求数列

(2)设



正确答案
解:
(1)∵


∴
当

当

∴
∴数列


∴
设



∴
(2)
∴
∴数列
∴
解析
解析已在路上飞奔,马上就到!
知识点
20.已知椭圆C方程为
(1)若直线AB的斜率为
(2)当A、B运动时,满足
正确答案
解:
(1)设





中整理得






四边形APBQ的面积


(2)当









同理2+







从而

解析
解析已在路上飞奔,马上就到!
知识点
22.选修4—5:不等式选讲
已知
正确答案
解:依题意得:
解析
解析已在路上飞奔,马上就到!
知识点
19.如图,在三棱锥









(1)求证:
(2)求二面角
正确答案
解:
(1)连结PD,






又




(2)法一:




则DE


DE
过D做DF垂直PB与F,连接EF,则EF 
∠DFE为所求二面角的平面角
则:DE=



法二:




如图,以D为原点建立空间直角坐标系








设平面PBE的法向量

得




设二面角的

由图知,
所以

解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数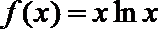
(1)证明:
(2)证明:
正确答案
解:
(1)令
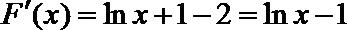
令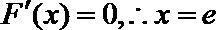
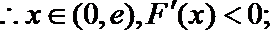
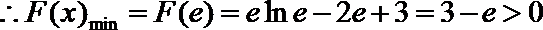
故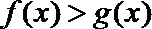
(2)由(1)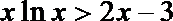
令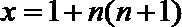
即
则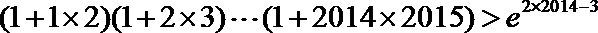
解析
解析已在路上飞奔,马上就到!
知识点
18.小白被“老大”找到了!小伙伴们喜大普奔啊有木有!为了答谢“老大”,小新他们决定帮助“老大”做一件事,就是调查双叶幼稚园小朋友在20:00~21:00时间段在做什么?最后小新等做成了下面的数据表:
(1)将此样本的频率作为总体的概率估计,随机调查3名男性小朋友,设调查的3名男性小朋友在这一时间段以看电视的人数为随机变量X,求X的分布列和期望;
(2)根据以上数据,吉永老师能否有99%的把握认为“在20:00~21:00时间段的休闲方式与性别有关系”?
参考公式: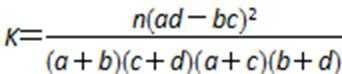
参考数据:
正确答案
解析
解析已在路上飞奔,马上就到!