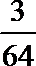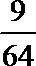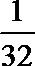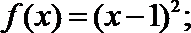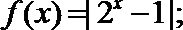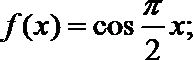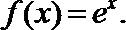理科数学济南市2011年高三试卷

精品

单选题
填空题
简答题

立即下载

理科数学热门试卷

X 查看更多试卷

试卷目录

1、单选题

2、填空题

3、简答题

真题试卷
模拟试卷
预测试卷

单选题本大题共12小题，每小题5分，共60分。在每小题给出的4个选项中，有且只有一项是符合题目要求。

题型：单选题

分值: 5分

1．已知集合=（）

B（-1，4）

D（2，4）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

集合的含义

题型：单选题

分值: 5分

7．在如图所示的流程图中，若输入值分别为，则输出的数为（）

D不确定

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

流程图的概念

题型：单选题

分值: 5分

8．为了得到函数的图象，可以将函数的图象（）

A向左平移个单位长度，再向下平移个单位长度

B向右平移个单位长度，再向上平移个单位长度

C向左平移个单位长度，再向下平移个单位长度

D向左平移个单位长度，再向上平移个单位长度

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：单选题

分值: 5分

9．已知两圆相交于两点A（1，3），B（t，-1），两圆圆心都在直线上，则t+c的值是（）

A-3

B-2

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

直线与椭圆的位置关系

题型：单选题

分值: 5分

3．若复数则mab的最大值是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

虚数单位i及其性质

题型：单选题

分值: 5分

4．不等式组所表示的平面区域的面积等于（）

B8.6

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

不等式的性质

题型：单选题

分值: 5分

5．下表是某工厂1~4月份用电量（单位：万度）的一组数据：

由散点图可知，用电量y与月份x间有较好的线性相关关系，其线性回归直线方程是，则a=（）

A10.5

B5.25

C5.2

D5.15

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：单选题

分值: 5分

6．已知为等差数列的前n项和，若=（）

A2011

B2010

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

由数列的前几项求通项

题型：单选题

分值: 5分

2．已知直线m，n和平面α，则m//n的必要不充分条件是（）

D与α成等角

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

充要条件的判定空间中直线与直线之间的位置关系

题型：单选题

分值: 5分

11．设函数定义在实数集上，对于任意的实数x，都有时，，则有（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：单选题

分值: 5分

12．已知点O是所在平面上一定点，动点M满足，则M点的轨迹一定通过（）

A垂心

B重心

C内心

D外心

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

四种命题及真假判断

题型：单选题

分值: 5分

10．一个质量均匀的正四面体型的模具，其四个面上分别标有数字1，2，3，4，若连续投掷三次，取三次面向上的数字分别作为三角形的边长，则其能构成钝角三角形的概率为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

排列、组合及简单计数问题古典概型的概率

填空题本大题共4小题，每小题4分，共16分。把答案填写在题中横线上。

题型：填空题

分值: 4分

13．设函数，则=___________。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：填空题

分值: 4分

16．对于函数，若存在区间（其中），使得则称区间M为函数的一个“稳定区间”。

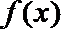
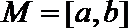
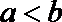
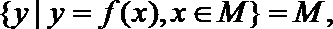
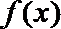
给出下列4个函数：

①

②

③

④

其中存在“稳定区间”的函数有___________（填出所有满足条件的函数序号）

正确答案

①②③

解析

解析已在路上飞奔，马上就到！

知识点

四种命题及真假判断

题型：填空题

分值: 4分

14．已知的二项展开式中，的系数为10，则a的值为___________。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：填空题

分值: 4分

15．双曲线的左、右焦分别是F1，F2，过F1作倾斜角为的直线交双曲线右支交于M点，若MF2垂直于x轴，则双曲线的离心率为 ___________。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

双曲线的几何性质直线与双曲线的位置关系

简答题（综合题）本大题共74分。简答应写出文字说明、证明过程或演算步骤。

题型：简答题

分值: 12分

18．某地区为下岗女职工免费提供财会和家政培训，以提高下岗女职工的再就业能力，每名下岗人员可以参加一项培训、参加两项培训或不参加培训，已知参加过财会培训的有50%，参加过家政培训的有80%，假设每个人对培训项目的选择是相互独立的，且各人的选择相互之间没有影响。

（I）任选1名下岗女职工，求该人参加过培训的概率；

（II）任选3名下岗女职工，记为3人中参加过培训的人数，求的分布列和期望。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

随机事件的关系

题型：简答题

分值: 12分

21．已知函数的导函数。

（I）若处取到极大值-2，求a，b的值；

（II）若函数，求函数的单调区间。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：简答题

分值: 12分

17．已知向量，且A、B、C分别为的三边a、b、c所对的角。

（1）求角C的大小；

（2）若三边a，c，b成等差数列，且求c边的长。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

由数列的前几项求通项

题型：简答题

分值: 12分

20．某旅游景点2010年利润为205万元，因市场竞争，若不开发新项目，预测从2011年起每年利润比上一年减少10万元，2011年初，该景点一次性投入150万元开发新项目，预测在未扣除开发所投入资金的情况下，第n年（n为正整数，2011年为第1年）的利润为万元。

（1）设从2011年起的前n年，该景点不开发新项目的累计利润为万元，开发新项目的累计利润为万元（须扣除开发所投入资金），求的表达式；

（2）依上述预测，该景点从第几年开始，开发新项目的累计利润超过不开发新项目的累计利润？

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：简答题

分值: 14分

22．已知点，过点D作抛线的切线，切点A在第一象限，如图。

（1）求切点A的纵坐标；

（2）若离心率为的椭圆恰好经过切点A，设切线交椭圆的另一点为B，记切线，OA，OB的斜率分别为，若，求抛物线C1和椭圆C2的方程。

（3）设P、Q分别是（2）中的椭圆C2的右顶点和上顶点，M是椭圆C2在第一象限的任意一点，求四边形OPMQ面积的最大值以及此时M点的坐标。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

双曲线的定义及标准方程

题型：简答题

分值: 12分

19．如图（a）所示，在边长为2的正方形ABB1A1中，C，C1分别是AB，A1B1的中点，现将正方形ABB1A1沿CC1折叠，使得平面ACC1A1平面CBB1C1，连接AB，A1B1，AB1，如图（b）所示，F是AB1的中点，E是CC1上的点。

（1）当E是棱CC1中点时，求证：平面ABB1A1；

（2）在棱CC1上是否存在点E，使得二面角A—EB1—B的大小为？若存在，求CE的长度；若不存在，请说明理由。

理科数学 热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

理科数学热门试卷