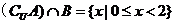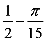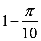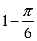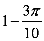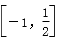- 真题试卷
- 模拟试卷
- 预测试卷
1.已知全集
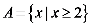
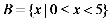
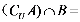
正确答案
解析
由题意易知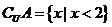
故选C.
知识点
5.已知某几何体的三视图(单位:cm)如图所示,则该几何体的体积是( )
正确答案
解析
如图所示,原几何体为:
一个长宽高分别为6,3,6的长方体砍去一个三棱锥,底面为直角边分别为3,4直角三角形,高为4.因此该几何体的体积=3×6×6﹣
知识点
3.复数

正确答案
解析
∵复数z=1﹣i,
∴





知识点
7.已知函数f(x)=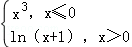
正确答案
解析
∵当x=0时,两个表达式对应的函数值都为零
∴函数的图象是一条连续的曲线
∵当x≤0时,函数f(x)=x3为增函数;当x>0时,f(x)=ln(x+1)也是增函数
∴函数f(x)是定义在R上的增函数
因此,不等式f(2﹣x2)>f(x)等价于2﹣x2>x,
即x2+x﹣2<0,解之得﹣2<x<1,
故选D。
知识点
8.以下判断正确的是( )
正确答案
解析
对于A,命题“负数的平方是正数”是全称命题,故A错误;
对于B,命题“

对于C,a=1时,函数f(x)=cos2x﹣sin2x=cos2x的最小正周期为T=
反之,若函数f(x)=cos2ax﹣sin2ax=cos2ax的最小正周期T=
所以“a=1”是函数f(x)=cos2ax﹣sin2ax的最小正周期为π的充分不必要条件,故C错误;
对于D,b=0时,函数f(﹣x)=ax2+bx+c=f(x),y=f(x)是偶函数,充分性成立;反之,若函数f(x)=ax2+bx+c是偶函数,f(﹣x)=f(x),解得a=0,即必要性成立;
所以“b=0”是“函数f(x)=ax2+bx+c是偶函数”的充要条件,故D正确.
故选:D.
知识点
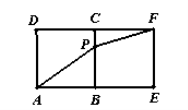
10.某同学为了研究函数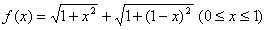
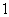
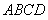
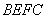
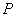
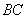
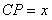
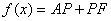
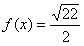
正确答案
解析
从图中知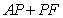
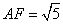
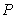
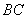
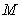
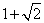
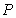
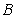
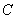
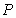
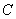
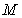
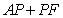
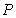
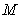
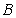
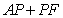
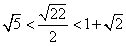
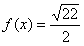
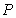
知识点
2.函数
正确答案
解析
因为


知识点
4.执行如图所示程序框图所表达的算法,若输出的x值为48,则输入的x值为( )
正确答案
解析
x←2x,n=1+1=2,满足n≤3,执行循环体;
x=2×(2x)=4x,n=2+1=3,满足n≤3,执行循环体;
x=2×(4x)=8x,n=3+1=4,不满足n≤3,退出循环体,
由8x=48即可得x=6.
则输入的x值为:6.
故选B.
知识点
6.一只受伤的丹顶鹤在如图所示(直角梯形)的草原上飞过其中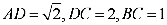
正确答案
解析
过点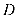
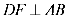
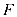
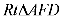
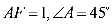
梯形的面积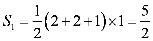
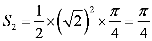
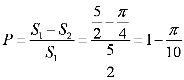
知识点
9.下列说法中正确的有( )
正确答案
解析
一组数据的平均数介于这组数据中的最大数据与最小数据之间,所以A错;众数是一组数据中出现最多的数据,所以可以不止一个,B错;若一组数据的个数有偶数个,则其中中位数是中间两个数的平均值,所以不一定是这组数据中的某个数据,C错;一组数据的方差越大,说明这组数据的波动越大,D对.
知识点
12.已知




正确答案
解析
略
知识点
13.已知

正确答案
解析
∵

∴

知识点
14.设函数

正确答案
1
解析
作出

知识点
15.若不等式|2x-1|+|x+2|≥a2+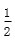
正确答案
解析
|2x-1|+|x+2|=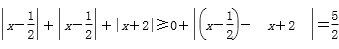
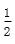
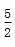
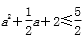
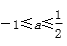
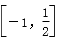
知识点
11.在平面直角坐标系xOy中,已知△ABC顶点A(﹣4,0)和C(4,0),顶点B在椭圆

正确答案
解析
利用椭圆定义得a+c=2×5=10b=2×4=8
由正弦定理得

知识点
16. 在数列{an}中,a1=

(1)求an,Sn;
(2)设bn=log2(2Sn+1)﹣2,数列{cn}满足cn•bn+3•bn+4=1+n(n+1)(n+2)•2bn,数列{cn}的前n项和为Tn,求使4Tn>2n+1﹣
正确答案
见解析。
解析
(1)由Sn=an+1﹣

两式作差得:an=an+1﹣an,即2an=an+1(n≥2),
∴
又
∴
∴数列{an}是首项为
则

(2)bn=log2(2Sn+1)﹣2=
∴cn•bn+3•bn+4=1+n(n+1)(n+2)•2bn,
即


=


由4Tn>2n+1﹣

即
∴使4Tn>2n+1﹣
知识点
19.从陕西某高校男生中随机抽取
(1)求
(2)按表1的身高组别进行分层抽样, 从这






正确答案
(1)


(2)
解析
(1)解:由
由

由

(2)解:依据分层抽样的方法,抽取的



而身高在区间


记“这



从身高不低于







事件






∴
知识点
21.已知

(1)讨论函数
(2)是否存在实数



(3)若方程


正确答案
见解析。
解析
(1)
(i)当a>0时,由ax2-1>0得 

故当a>0时,F(x)的递增区间为

(ii)当

(2)即使
(i)当a≤0时,由(1)知当
∴
(ii)当a>0时,由(1)可知

故存在这样的a的值,使得
a的取值范围是
(3)等价于方程

∵





所以 a的取值范围是
知识点
17.在△ABC中,角A,B,C的对边分别为a,b,c.已知,
(1)求证:
(2)若
正确答案
见解析。
解析
(1)由 

即
整理得:

所以
(2)由(1)及

所以
所以三角形ABC的面积
知识点
18.如图,三棱柱ABC﹣A1B1C1中,侧面AA1C1C⊥底面ABC,AA1=A1C=AC=2,AB=BC且AB⊥BC.
(1)求证:AC⊥A1B;
(2)求三棱锥C1﹣ABA1的体积.
正确答案
见解析。
解析
(1)证明:取AC中点O,连A1O,BO.
∵AA1=A1C,∴A1O⊥AC,
又AB=BC,∴BO⊥AC,
∵A1O∩BO=O,∴AC⊥平面A1OB,
又A1B⊂平面A1OB,
∴AC⊥A1B
(2)解:由条件得:
∵三棱柱ABC﹣A1B1C1中,侧面AA1C1C⊥底面ABC,
AA1=A1C=AC=2,AB=BC且AB⊥BC,
∴

∴
=
知识点
20.设椭圆




离心率,
(1)求椭圆
(2)过椭圆右焦点




正确答案
见解析。
解析
(1)
(2)因为
若直线




若直线



联立
又∵
∴