- 真题试卷
- 模拟试卷
- 预测试卷
1.已知
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2. 设A={三角形},B={圆},建立对应法则f是对三角形作外接圆,下列说法正确的个数是( )
①不是A到B的映射
②是A到B的映射
③是A到B的一一映射
④是A到B的函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.命题“存在

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.化简:
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.已知函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8. 已知函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9. 

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12. 在实数的原有运算法则中,我们补充定义新运算“
当

当

则函数
(“·”和“-”仍为通常的乘法和减法)
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.为了得到函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11. 定义在R上的函数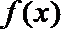
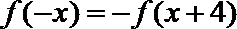
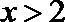
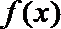
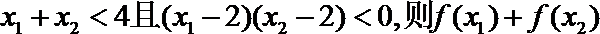
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.曲线
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.
正确答案
1
解析
解析已在路上飞奔,马上就到!
知识点
14.函数y=
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.定义在R上的函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.若存在过点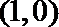
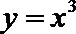
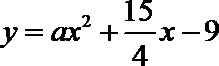
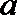
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.已知p:∀x∈R,2x>m(x2+1),q:∃x0∈R,x+2x0-m-1=0,且p∧q为真,求实数m的取值范围。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.已知定义域为R的函数
(1)求
(2)若对任意的


正确答案
(1)因为


又由f(1)= -f(-1)知
(2)由(1)知


又因
等价于
因

即对一切

解析
解析已在路上飞奔,马上就到!
知识点
19.设
(1)若

(2)若

正确答案
(2)由
令

只需
由
∵


综上k的取值范围为
解析
解析已在路上飞奔,马上就到!
知识点
20.已知集合
(1)判断函数




(2)若函数

正确答案
(1)由条件可得



同理
(2)若
①当

定义域为

所以:
②当

得

而此时值域为

②当

得

而值域为
若定义域和值域相等,则
解得:
综上所述:
解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数



(Ⅰ)当函数



(Ⅱ)在(Ⅰ)的条件下,当


(Ⅲ)若






正确答案
(Ⅰ)因为

因为方程

所以


所以
(Ⅱ)因为
=
所以当 

即


(Ⅲ)


所以
因为


又因为

所以
此时
所以
解析
解析已在路上飞奔,马上就到!
知识点
22.设函数
(1)求
(2)若
(3)若存在



正确答案
略
解析
解析已在路上飞奔,马上就到!