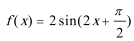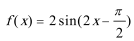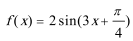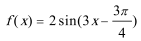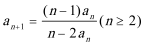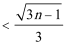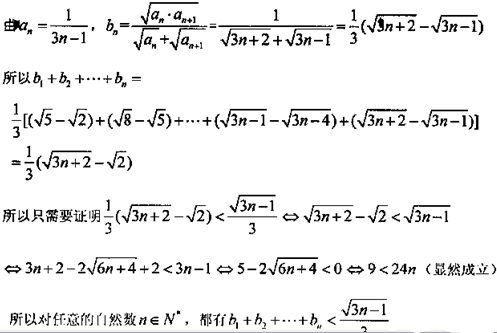理科数学合肥市2013年高三试卷

精品

单选题
填空题
简答题

立即下载

理科数学热门试卷

X 查看更多试卷

试卷目录

1、单选题

2、填空题

3、简答题

真题试卷
模拟试卷
预测试卷

单选题本大题共10小题，每小题5分，共50分。在每小题给出的4个选项中，有且只有一项是符合题目要求。

题型：单选题

分值: 5分

5．已知函数的部发图象如图所示，则函数的解析式为（）

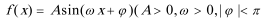
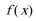
正确答案

解析

解析已在路上飞奔，马上就到！

知识点

由y=Asin（ωx+φ）的部分图象确定其解析式

题型：单选题

分值: 5分

7．将函数y=sin2x的图像上所有的点向右平行移动个单位长度，再把所得各点的横坐标缩短到原来的倍（纵坐标不变），则所得函数的图象（　　）

A关于点对称

B关于直线对称

C关于点对称

D关于直线对称

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

正弦函数的对称性函数y=Asin（ωx+φ）的图象变换

题型：单选题

分值: 5分

8．函数满足当x时，则的图象与的图象的交点共有（　　）

A3个

B4个

C5个

D6个

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

对数函数的图像与性质函数零点的判断和求解

题型：单选题

分值: 5分

3．设x，y满足约束条件，则的最小值为（）

C－7

D－6

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

不等式的性质

题型：单选题

分值: 5分

6．已知数列{an}的前n项和则=（　　）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

由an与Sn的关系求通项an

题型：单选题

分值: 5分

10．已知是三次函数的两个极值点，且则的取值范围是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：单选题

分值: 5分

4．设{an}是公差为正数的等差数列，若a1+a2+a3=15，a1a2a3=80，则a11+a12+a13=（　　）

A120

B105

C90

D75

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

由数列的前几项求通项

题型：单选题

分值: 5分

2．已知集合则（）

B（0，1）

D（－1，1）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

题型：单选题

分值: 5分

1．复数（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

复数的代数表示法及其几何意义

题型：单选题

分值: 5分

9．已知函数在R上满足%）－，则曲线在点处的切线方程是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的几何意义

填空题本大题共5小题，每小题5分，共25分。把答案填写在题中横线上。

题型：填空题

分值: 5分

11．已知正数x，y满足则的最小值为（）。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

利用基本不等式求最值

题型：填空题

分值: 5分

14．数列{an}的前n项和为Sn，且则（）。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

由数列的前几项求通项

题型：填空题

分值: 5分

12．已知点G是△ABC的重心，且···则

（）。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

余弦定理向量在几何中的应用

题型：填空题

分值: 5分

13．已知则（）。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

两角和与差的正弦函数角的变换、收缩变换

题型：填空题

分值: 5分

15．下列命题中是真命题的是（）（写出所有你认为是真命题的序号）

①命题命题则是真命题；

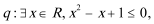
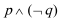
②若不等式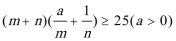对恒成立，则a的最小值为16；

③函数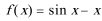的零点有3个；

④若函数的图像关于y轴对称，则；

⑤“a，b，c成等比数列”是的充要条件。

正确答案

①②

解析

解析已在路上飞奔，马上就到！

知识点

四种命题及真假判断

简答题（综合题）本大题共75分。简答应写出文字说明、证明过程或演算步骤。

题型：简答题

分值: 13分

19．在数列{an}中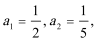且

（1）求a3、a4，并求出数列{an}的通项公式；

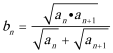
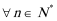
（2）设，求证：对，都有b1+b2+……bn

正确答案

（1）

（2）

解析

解析已在路上飞奔，马上就到！

知识点

由递推关系式求数列的通项公式

题型：简答题

分值: 12分

18．函数在处取得极值，其中a，b为常数。

（1）求实数a的值；

（2）若对不等式恒成立，求实数b的取值范围。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

变化的快慢与变化率

题型：简答题

分值: 13分

21．设Tn为数列{an}的前n项乘积，满足

（1）设，求证：数列{bn}是等差数列；

（2）设·，求证数列{cn}的前n项和；

（3）设求证：

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

由an与Sn的关系求通项an

题型：简答题

分值: 12分

17．设函数。

（1）求的值域；

（2）记△ABC的内角A，B，C所对边长分别为a，b，c，若，c=3，求a的值。

正确答案

（1）

（2）

解析

解析已在路上飞奔，马上就到！

知识点

指数函数的图像与性质

题型：简答题

分值: 13分

20．已知函数

（1）求的单调区间；

（2）若在上的最小值是0，求实数a的取值范围。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的图像

题型：简答题

分值: 12分

16．△ABC的内角A，B，C把对的边a，b，c且ccosB与bcosC的等差中项为2acosA。

（1）求cosA的值；

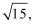
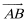
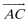
（2）若△ABC的面积是求·的值。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

诱导公式的推导

理科数学 热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

理科数学热门试卷