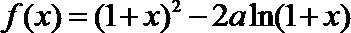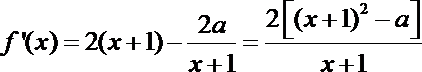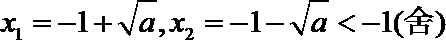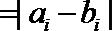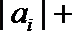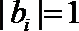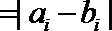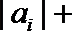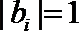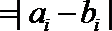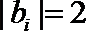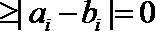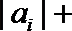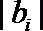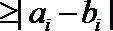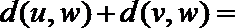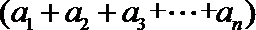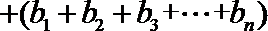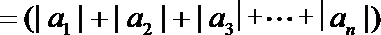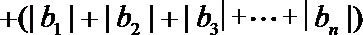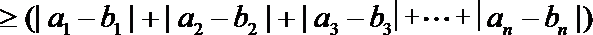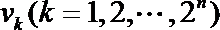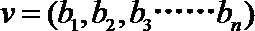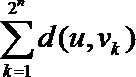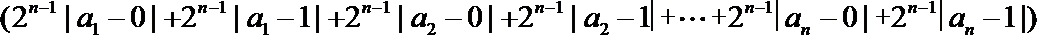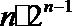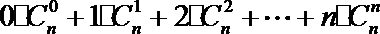- 真题试卷
- 模拟试卷
- 预测试卷
5. 函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6. 设






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4. 为了得到函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7. 已知


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1. 设集合


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3. 已知i是虚数单位,


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.设
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8. 设



① 
② 既不是奇函数也不是偶函数;
③ 

④ 存在经过点

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知实数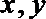
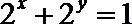
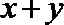
正确答案
-2
解析
解析已在路上飞奔,马上就到!
知识点
9. 在等差数列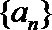
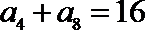
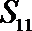
正确答案
88
解析
解析已在路上飞奔,马上就到!
知识点
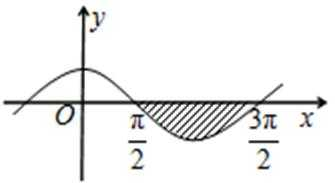
10.如图,阴影区域是由函数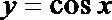
正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
11.在△






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.若直线



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.设集合







① 
② 
⑤ 
④ 整数集
以0为聚点的集合有__________ .(请写出所有满足条件的集合的编号)
正确答案
②③
解析
解析已在路上飞奔,马上就到!
知识点
16.已知数列






(1)求数列

(2)设




正确答案
(1)由


所以数列

于是

当
当


又



(2)由(Ⅰ)知



所以
等式两边同乘以

(1)-(2)得
所以
解析
解析已在路上飞奔,马上就到!
知识点
17.已知函数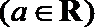
(Ⅰ)求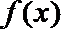
(Ⅱ)若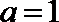
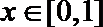
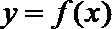
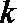
正确答案
解:(Ⅰ)函数的定义域为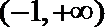
当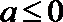
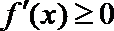

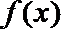
当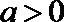
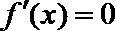
当
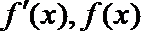
所以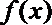
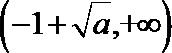
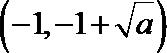
综上,当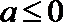
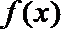
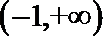
当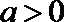
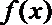
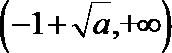
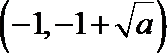
(Ⅱ)当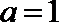
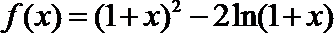
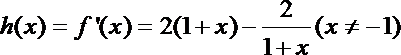
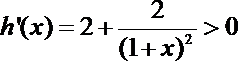
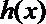
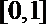
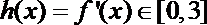
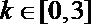
解析
解析已在路上飞奔,马上就到!
知识点
19.已知函数
(1)若

(2)若

正确答案
(1)解:
因为x = 2为f (x)的极值点,所以
即
又当a = 0时,


从而x = 2为f (x)的极值点成立.
(2)解:∵f (x)在区间[3,+∞)上为增函数,
∴
①当a = 0时,
②当a > 0时,
令

∵a > 0,∴
由

∵a > 0,∴
综上所述,a的取值范围为[0,
解析
解析已在路上飞奔,马上就到!
知识点
20.已知
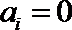
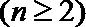
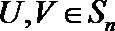
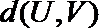
(Ⅰ)令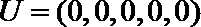
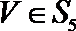
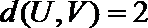
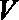
(Ⅱ)令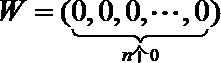
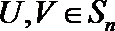
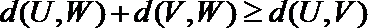
(Ⅲ)给定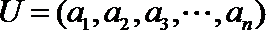
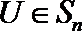
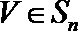
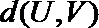
正确答案
解:(Ⅰ)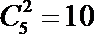
(Ⅱ)证明:令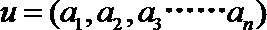
∵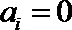
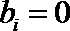
当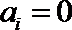
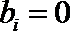
当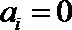
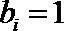
当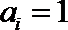
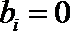
当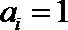
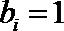
故
∴
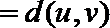
(Ⅲ)解:易知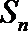
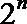
∵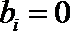
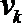
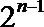
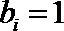
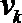
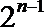
∴
=
=
∴
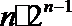
法二:根据(Ⅰ)知使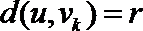
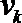
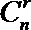
∴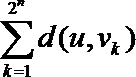
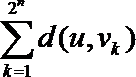
两式相加得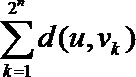
解析
解析已在路上飞奔,马上就到!
知识点
15.已知函数

(1)求函数
(2)求函数

正确答案
解: 
(1)
令

所以函数

(2)因为


于是 

当且仅当

当且仅当


解析
解析已在路上飞奔,马上就到!
知识点
18.如图,游客从某旅游景区的景点






















(Ⅰ)问乙出发多少分钟后,乙在缆车上与甲的距离最短?
(Ⅱ)为使两位游客在

正确答案
解: (Ⅰ)∵




∴
根据

所以乙在缆车上的时间为
设乙出发


则
∴

(Ⅱ)由正弦定理

乙从

设乙步行速度为
则

∴为使两位游客在


解析
解析已在路上飞奔,马上就到!