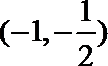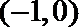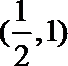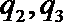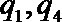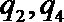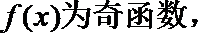- 真题试卷
- 模拟试卷
- 预测试卷
2．已知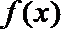
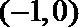
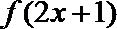
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
3．不等式
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
4．设
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
5．已知命题p1：函数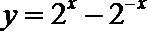
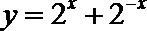
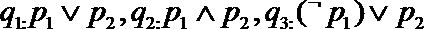
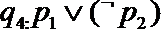
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
6．下列函数
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
8．函数
A（
B（
C（
D（
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
1．已知集合
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
7． 已知图1是函数
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
9．曲线
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
10．若函数
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
11．已知函数
①
②函数
③若
④若
正确的个数有（ ）
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
12．对任意实数a，b定义运算
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
13．已知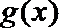
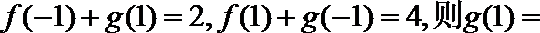
正确答案
3
解析
解析已在路上飞奔，马上就到！
知识点
15．方程x3－3x＝k有3个不等的实根， 则常数k的取值范围是______．
正确答案
（-2，2）
解析
解析已在路上飞奔，马上就到！
知识点
14．已知集合
正确答案
4
解析
解析已在路上飞奔，马上就到！
知识点
16．若
正确答案
-18
解析
解析已在路上飞奔，马上就到！
知识点
19．已知命题
正确答案
∵方程
显然
∵
∴
只有一个实数满足
∴ 
∴命题
∵命题
∴
解析
解析已在路上飞奔，马上就到！
知识点
17．已知二次函数f（x）=ax2﹣4x+c．若f（x）＜0的解集是（﹣1，5）
（1）求实数a，c的值；
（2）求函数f（x）在x∈[0，3]上的值域．
正确答案
（1）由f（x）＜0，得：ax2﹣4x+c＜0，
不等式ax2﹣4x+c＜0的解集是（﹣1，5），
故方程ax2﹣4x+c=0的两根是x1=﹣1，x2=5．
所以
所以a=1，c=﹣5．
（2）由（1）知，f（x）=x2﹣4x﹣5=（x﹣2）2﹣9．
∵x∈[0，3]，f（x）在[0，2]上为减函数，在[2，3]上为增函数．
∴当x=2时，f（x）取得最小值为f（2）=﹣9．
而当x=0时，f（0）=（0﹣2）2﹣9=﹣5，当x=3时，f（3）=（3﹣2）2﹣9=﹣8
∴f（x）在[0，3]上取得最大值为f（0）=﹣5．
∴函数f（x）在x∈[0，3]上的值域为[﹣9，﹣5]．
解析
解析已在路上飞奔，马上就到！
知识点
18．设曲线
（1）当
（2）求
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
20．某商场销售某种商品的经验表明，该商品每日的销售量
（1）求
（2）若该商品的成本为3元/千克，试确定销售价格
正确答案
（1）因为
（2）由（1）可知，该商品每日的销售量
所以商场每日销售该商品所获得利润
从而
于是，当
由表知，
所以当
解析
解析已在路上飞奔，马上就到！
知识点
21．设
（1）当
（2）当
正确答案
（1）由题意知
且
由
当
（2）要使
即
（i）当
（ii）当
（iii）当
解得：
解析
解析已在路上飞奔，马上就到！
知识点
22．已知函数f（x）=x3-ax2-3x．
（1）若f（x）在区间［1，+∞）上是增函数，求实数a的取值范围；
（2）若x= -
（3）在（2）的条件下，是否存在实数b，使得函数g（x）=bx的图象与函数f（x）的图象恰有3个交点，若存在，请求出实数b的取值范围；若不存在，试说明理由．
正确答案
（1）
∴ 
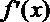
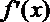
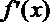
即3x2-2ax-3≥0在［1，+∞）上恒成立．
则必有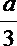
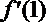
∴ a≤0．
（2）依题意，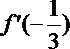
∴ a=4，∴ f（x）=x3-4x2-3x．
令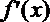
则当x变化时，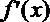
∴ f（x）在［1，4］上的最大值是f（1）=-6．
（3）函数g（x）=bx的图象与函数f（x）的图象恰有3个交点，
即方程x3-4x2-3x=bx恰有3个不等实根
∴ x3-4x2-3x-bx=0，∴x=0是其中一个根
∴ 方程x2-4x-3-b=0有两个非零不等实根，
∴
∴ 存在符合条件的实数b，b的范围为b>-7且b≠-3．
解析
解析已在路上飞奔，马上就到！