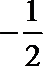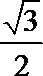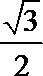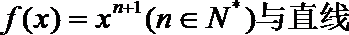- 真题试卷
- 模拟试卷
- 预测试卷
3.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知各项均不为零的数列

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.若sin2x、sinx分别是sinθ与cosθ的等差中项和等比中项,则cos2x的值为 ( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.如图是函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.在下图的表格中,如果每格填上一个数后,每一横行成等差数列,每一纵列成等比数列,那么x+y+z的值为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知函数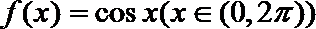
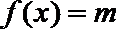
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.已知点A(-1,1),点B(2,y),向量a=(l,2),若
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.已知等比数列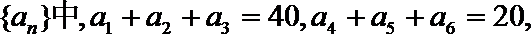
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.设函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.设函数f(x) =ex(sinx—cosx),若0≤x≤2012π,则函数f(x)的各极大值之和为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.设
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.由下面四个图形中的点数分别给出了四个数列的前四项,将每个图形的层数增加可得到这四个数列的后继项,按图中多边形的边数依次称这些数列为“三角形数列”、“四边形数列”…,将构图边数增加到n可得到“n边形数列”,记它的第r项为P(n,r),则
(1)使得P(3,r)>36的最小r的取值是____;
(2)试推导P(n,r)关于,n、r的解析式是____.
正确答案
(1)
(2)

解析
解析已在路上飞奔,马上就到!
知识点
13.已知
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.如图放置的正方形ABCD,AB =1.A,D分别在x轴、y轴的正半轴(含原点)上滑动,则
正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
12.已知曲线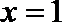
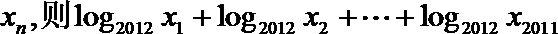
正确答案
-1
解析
解析已在路上飞奔,马上就到!
知识点
16.已知

(1)若

(2)若函数y=f(x)的定义域为[
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.如图,某测量人员,为了测量西江北岸不能到达的两点A,B之间的距离,她在西江南岸找到一个点C,从C点可以观察到点A,B;找到一个点D,从D点可以观察到点A,C;到一个点E,从E点可以观察到点B,C;并测量得到数据:∠ACD=90°,∠ADC= 60°,∠ACB =15°,∠BCE =105°,∠CEB =45°,DC=CE =1(百米).
(1)求△CDE的面积;
(2)求A,B之间的距离.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知
(I)求证:数列{an,-1)是等比数列;
(Ⅱ)当n取何值时,bn取最大值,并求出最大值;
(Ⅲ)若
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.国家助学贷款是由财政贴息的信用贷款,旨在帮助高校家庭经济困难学生支付在校学习期间所需的学费、住宿费及生活费.每一年度申请总额不超过6000元.某大学2010届毕业生李顺在本科期间共申请了24000元助学贷款,并承诺在毕业后3年内(按36个月计)全部还清.
签约的单位提供的工资标准为第一年内每月1500元,第13个月开始,每月工资比前一个月增加5%直到4000元.李顺同学计划前12个月每个月还款额为500元,第13个月开始,每月还款额比前一月多x元.
(1)若李顺恰好在第36个月(即毕业后三年)还清贷款,求x的值;
(2)当x=50时,李顺同学将在第几个月还清最后一笔贷款?他还清贷款的那一个月的工资余额是多少?
(参考数据:1.0518 =2.406,1.0519=2.526,1.0520 =2.653,1.0521=2.786)
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知函数
(I)当
(II)设
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.设曲线C:
(I)求函数f(x)的极值;
(Ⅱ)数列{an}满足
(Ⅲ)对于曲线C上的不同两点A(x1,y1),B (x2,y2),x1<x2,求证:存在唯一的
正确答案
解析
解析已在路上飞奔,马上就到!