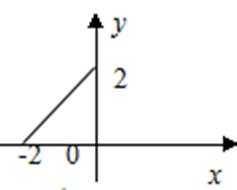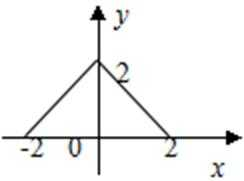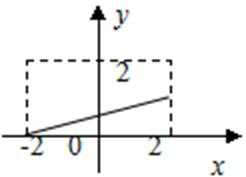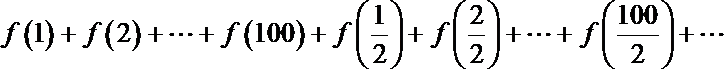- 真题试卷
- 模拟试卷
- 预测试卷
5. 设函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.如果0<a<1,那么下列不等式中正确的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.将函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.若x∈R、n∈N*,定义: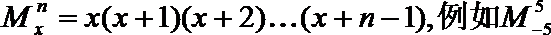
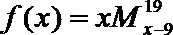
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.给定实数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.集合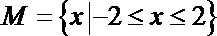

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3. 设正方体的棱长为,则它的外接球的表面积为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.定义运算

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.设




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.定义在R上的偶函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.定义在R上的函数





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.下列函数中,在其定义域内既是奇函数又是减函数的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知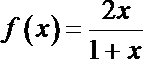
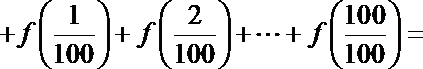
正确答案
10000
解析
解析已在路上飞奔,马上就到!
知识点
13.计算
正确答案
11
解析
解析已在路上飞奔,马上就到!
知识点
14.若曲线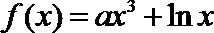

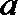
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.设曲线



正确答案
-2
解析
解析已在路上飞奔,马上就到!
知识点
17.己知函数

函数


(1) 求A
(2)若同时满足A,B的

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.如图所示是一个几何体的直观图、正视图、俯视图、侧视图(其中正视图为直角梯形,俯视图为正方形,侧视图为直角三角形,尺寸如图所示)

(Ⅰ)求四棱锥

(Ⅱ)证明:

(Ⅲ) 若G为BC上的动点,求证:
正确答案
解:(Ⅰ) 由几何体的三视图可知,底面








(Ⅱ) 连接













又




(Ⅲ)连BP,





又




解析
解析已在路上飞奔,马上就到!
知识点
20. 设函数

(1)求
(2)判断并证明函数

(3)若直线







正确答案
解:(1)由




(2)任取







∴

(3)当直线




∴




得:



解析
解析已在路上飞奔,马上就到!
知识点
21.已知一家公司生产某种品牌服装的年固定成本为10万元,每生产1千件需另投入2.7万元。设该公司一年内共生产该品牌服装x千件并全部销售完,每千件的销售收入为R(x)万元,且
(1)写出年利润W(万元)关于年产量x(千件)的函数解析式;
(2)年产量为多少千件时,该公司在这一品牌服装的生产中所获得利润最大?
(注:年利润=年销售收入—年总成本)
正确答案
解:(1)当

(2)①当
②当
综合①②知当
解析
解析已在路上飞奔,马上就到!
知识点
19.已知函数

(1)求常数a、b的值;
(2)求函数


正确答案
(1)
(2)









解析
解析已在路上飞奔,马上就到!
知识点
22.已知函数




(1) 求
(2) 设


(3)是否存在实数a,使得当

正确答案
(1)设

又因为

故函数
(2)证明:当


因为






又因为




所以当

(3)解:假设存在实数


(ⅰ)当





(ⅱ)当





(ⅲ)当




所以

(ⅳ)当
当


当


所以

综上可知,存在实数


解析
解析已在路上飞奔,马上就到!