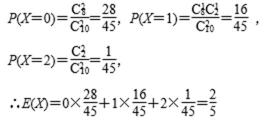- 真题试卷
- 模拟试卷
- 预测试卷
3.一次函数
正确答案
解析
因为


知识点
4.某市A,B,C,D四所中学报名参加某高校今年自主招生的学生人数如下表所示:
为了了解参加考试的学生的学习状况,该高校采用分层抽样的方法从报名参加考试的四所中学的学生当中随机抽取50名参加问卷调查,则A,B,C,D四所中学,抽取学生数分别是多少名( )
正确答案
解析
由题意知,四所中学报名参加该高校今年自主招生的学生总人数为100,抽取的样本容量与总体个数的比值为=
知识点
7.已知△ABC中,内角A,B,C所对边长分别为a,b,c,若A=,b=2acos B,c=1,则△ABC的面积等于( )
正确答案
解析
由正弦定理得sin B=2sin Acos B,故tan B=2sin A=



知识点
8.已知函数f(x)=
正确答案
解析
由题意可知,函数f(x)是R上的减函数,
于是有
由此解得a≤
即实数a的取值范围是
知识点
10.已知函数f(x)的定义域为R,且f(x)=
正确答案
解析
x≤0时,
f(x)=2-x-1,
0<x≤1时,-1<x-1≤0,
f(x)=f(x-1)=2-(x-1)-1.
故x>0时,f(x)是周期函数,
如图所示.
若方程f(x)=x+a有两个不同的实数根,则函数f(x)的图象与直线y=x+a有两个不同交点,
故a<1,即a的取值范围是(-∞,1),故选A.
知识点
1.设集合A={(x,y)|x+y=1},B={(x,y)|x-y=3},则满足M⊆(A∩B)的集合M的个数是( )
正确答案
解析
由题中集合可知,集合A表示直线x+y=1上的点,集合B表示直线x-y=3上的点,联立
知识点
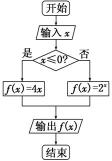
2.根据给出的程序框图,计算f(-1)+f(2)=( )
正确答案
解析
输入-1,满足x≤0,所以f(-1)=4×(-1)=-4;
输入2,不满足x≤0,所以f(2)=22=4,
即f(-1)+f(2)=0.故选A.
知识点
5.任取实数a,b∈[-1,1],则a,b满足|a-2b|≤2的概率为( )
正确答案
解析
如图所示,则事件|a-2b|≤2所表示的区域为图中的阴影部分所表示的区域,易知直线a-2b=-2分别交直线a=-1与y轴于点
所以|BE|=
所以S△BEF=



易得△DHG≌△BEF.
因此S△DHG=S△BEF=
故阴影部分的面积
S=S四边形ABCD-2S△BEF=22-2×

由几何概型的概率公式可知,事件|a-2b|≤2的概率

知识点
6.若命题“∃x0∈R,x+(a-1)x0+1<0”是真命题,则实数a的取值范围是( )
正确答案
解析
因为命题“∃x0∈R,x+(a-1)x0+1<0”等价于x+(a-1)x0+1=0有两个不等的实根,所以Δ=(a-1)2-4>0,即a2-2a-3>0,解得a<-1或a>3,故选D.
知识点
9.将进货单价为80元的商品按90元出售时,能卖出400个.若该商品每个涨价1元,其销售量就减少20个,为了赚取最大的利润,售价应定为每个( )
正确答案
解析
设售价定为(90+x)元,卖出商品后获得利润为:y=(90+x-80)(400-20x)=20(10+x)(20-x)=20(-x2+10x+200)=-20(x2-10x-200)=-20[(x-5)2-225],∴当x=5时,y取得最大值,即售价应定为:90+5=95(元),选C.
知识点
14.已知函数f(x)=
正确答案

解析
依题意得,f1(x)=
f2(x)=


f3(x)=


由此归纳可得fn(x)=
知识点
11.已知双曲线
正确答案
解析
由题意,c=
∴a2+b2=c2=25. ①
又双曲线的渐近线为y=±


则由①②解得a=3,b=4,∴双曲线方程为
知识点
12.一个圆锥过轴的截面为等边三角形,它的顶点和底面圆周在球O的球面上,则该圆锥的体积与球O的体积的比值为________.
正确答案
解析
设等边三角形的边长为2a,则V圆锥=




知识点
13.在数列{an}中,a1=1,an+2+(-1)nan=1,记Sn是数列{an}的前n项和,则S60=________.
正确答案
480
解析
依题意得,当n是奇数时,an+2-an=1,即数列{an}中的奇数项依次形成首项为1,公差为1的等差数列,a1+a3+a5+…+a59=30×1+
知识点
15.若|x-1|≤1,|y-2|≤1,则|x-2y+1|的最大值为________.
正确答案
5
解析
|x-2y+1|=|(x-1)-2(y-2)-2|≤|x-1|+2|y-2|+2=5.
知识点
18.如图,在四棱锥PABCD中,PC⊥底面ABCD,底面ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2,E是PB的中点.
(1)求证:平面EAC⊥平面PBC;
(2)若二面角PACE的余弦值为
正确答案
见解析。
解析
(1)证明:∵PC⊥底面ABCD,∴PC⊥AC,
∵底面ABCD是直角梯形,且AB=2AD=2CD=2,
∴AC=

∴AB2=AC2+BC2,
∴AC⊥BC,
∵PC∩BC=C,∴AC⊥平面PBC,
∵AC⊂平面EAC,
∴平面EAC⊥平面PBC.
(2)建立如图所示的空间直角坐标系Axyz.设PC=a,则A(0,0,0),C(1,1,0), 
∴




设平面EAC的法向量为v=(x,y,z),
则即令x=1,
则v=
∵BC⊥平面PAC,
∴平面PAC的一个法向量为u=
设二面角PACE的大小θ,
则cos θ=
解得a=2,
∴直线PA与平面EAC所成角的正弦值为
cos〈v,
知识点
17.已知数列{an}满足a1=5,a2=5,an+1=an+6an-1(n≥2).
(1)求证:{an+1+2an}是等比数列;
(2)求数列{an}的通项公式.
正确答案
见解析。
解析
(1)证明:∵an+1=an+6an-1(n≥2),
∴an+1+2an=3an+6an-1=3(an+2an-1)(n≥2).
又a1=5,a2=5,
∴a2+2a1=15,
∴an+2an-1≠0(n≥2),
∴
∴数列{an+1+2an}是以15为首项,3为公比的等比数列.
(2)由(1)得an+1+2an=15×3n-1=5×3n,
则an+1=-2an+5×3n,
∴an+1-3n+1=-2(an-3n).
又∵a1-3=2,∴an-3n≠0,
∴{an-3n}是以2为首项,-2为公比的等比数列.
∴an-3n=2×(-2)n-1,
即an=2×(-2)n-1+3n(n∈N*).
知识点
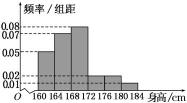
19.某市一次全市高中男生身高统计调查数据显示:全市100 000名男生的身高服从正态分布N(168,16).现从某学校高三年级男生中随机抽取50名测量身高,测量发现被测学生身高全部介于160 cm和184 cm之间,将测量结果按如下方式分成6组:第1组[160,164),第2组[164,168),…,第6组[180,184],如图是按上述分组方法得到的频率分布直方图.
(1)试评估该校高三年级男生在全市高中男生中的平均身高状况;
(2)求这50名男生身高在172 cm以上(含172 cm)的人数;
(3)在这50名男生身高在172 cm以上(含172 cm)的人中任意抽取2人,将该2人中身高排名(从高到低)在全市前130名的人数记为X,求X的数学期望.
参考数据:
若X~N(μ,σ2),则
P(μ-σ<X≤μ+σ)=0.682 6,
P(μ-2σ<X≤μ+2σ)=0.954 4,
P(μ-3σ<X≤μ+3σ)=0.997 4.
正确答案
见解析。
解析
(1)由频率分布直方图,经过计算得该校高三年级男生平均身高为
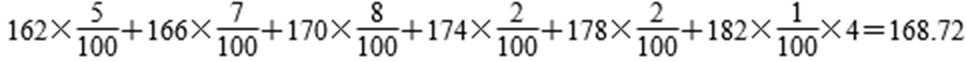
高于全市的平均值168.
(2)由频率分布直方图知,后3组频率为(0.02+0.02+0.01)×4=0.2,人数为0.2×50=10,即这50名男生身高在172 cm以上(含172 cm)的人数为10.
(3)∵P(168-3×4<X≤168+3×4)=0.997 4,
∴P(X≥180)=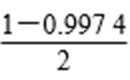
∴全市前130名的身高在180 cm以上,这50人中180 cm以上的有2人.
随机变量X可取0,1,2,于是
知识点
20.已知椭圆方程为+x2=1,斜率为k(k≠0)的直线l过椭圆的上焦点且与椭圆相交于P,Q两点,线段PQ的垂直平分线与y轴相交于点M(0,m).
(1)求m的取值范围;
(2)求△MPQ面积的最大值.
正确答案
(1)
(2)
解析
(1)设直线l的方程为y=kx+1,
由
设P(x1,y1),Q(x2,y2),
则x1+x2=

可得y1+y2=k(x1+x2)+2=
设线段PQ的中点为N,则点N的坐标为
由题意有kMN·k=-1,可得
可得m=

故m的取值范围为
(2)设椭圆的焦点为F,由(1)可得k2=
所以△MPQ的面积为
设f(m)=m(1-m)3,则f′(m)=(1-m)2(1-4m).
可知f(m)在区间

所以,当m=
即当m=
知识点
16.在△ABC中,角A,B,C所对的边分别为a,b,c,cos 2C+
(1)求角C的大小;
(2)若b=

正确答案
(1)
(2)
解析
(1)∵cos 2C+
∴2cos2C+
即(

又C∈(0,π),∴C=
(2)∵c2=a2+b2-2abcos C=3a2+2a2=5a2,
∴c=



∵S△ABC=

∴absin C=
∴sin C=

解得c=1.
知识点
21.已知f(x)=ex(x3+mx2-2x+2).
(1)假设m=-2,求f(x)的极大值与极小值;
(2)是否存在实数m,使f(x)在
正确答案
见解析。
解析
(1)当m=-2时,
f(x)=ex(x3-2x2-2x+2),其定义域为(-∞,+∞).
则f′(x)=ex(x3-2x2-2x+2)+ex(3x2-4x-2)
=xex(x2+x-6)
=(x+3)x(x-2)ex,
∴当x∈(-∞,-3)或x∈(0,2)时,f′(x)<0;
当x∈(-3,0)或x∈(2,+∞)时,f′(x)>0;
f′(-3)=f′(0)=f′(2)=0,
∴f(x)在(-∞,-3)上单调递减,在(-3,0)上单调递增;
在(0,2)上单调递减,在(2,+∞)上单调递增,
∴当x=-3或x=2时,f(x)取得极小值;
当x=0时,f(x)取得极大值,
∴f(x)极小值=f(-3)=-37e-3,f(x)极小值=f(2)=-2e2,
f(x)极大值=f(0)=2.
(2)f′(x)=ex(x3+mx2-2x+2)+ex(3x2+2mx-2)
=
∵f(x)在
∴当x∈
又∵当x∈
∴当x∈
∴
∴当m∈