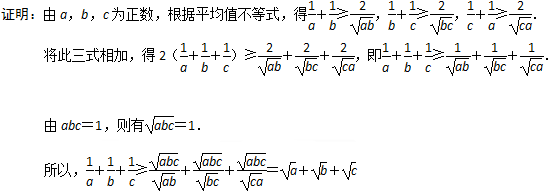- 真题试卷
- 模拟试卷
- 预测试卷
2.若复数 
正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
1.设集合A={x|-1<x<2},B={x|0<x<4,x∈N},则A∩B=( )
正确答案
{1}
解析
解析已在路上飞奔,马上就到!
知识点
4.如图是一个算法流程图,则输出的S的值是( )
正确答案
5
解析
解析已在路上飞奔,马上就到!
知识点
7.函数
正确答案
[-
解析
解析已在路上飞奔,马上就到!
知识点
8.设实数x,y,b满足
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知α,β表示两个不同的平面,m为平面α内的一条直线,则“α⊥β”是“m⊥β”的( )条件。(填“充分不必要”、“必要不充分”、“充要”或“既不充分也不必要”)
正确答案
必要不充分
解析
解析已在路上飞奔,马上就到!
知识点
10.设函数f(x)是定义在R上的偶函数,且在区间[0,+∞)上单调递增,则满足不等式f(1)<f(lg(2x))的x的取值范围是( )
正确答案
(0,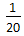
解析
解析已在路上飞奔,马上就到!
知识点
3.某时段内共有100辆汽车经过某一雷达测速区域,将测得的汽车时速绘制成如图所示的频率分布直方图。根据图形推断,该时段时速超过50km/h的汽车辆数为( )
正确答案
77
解析
解析已在路上飞奔,马上就到!
知识点
5.一只口袋内装有大小相同的5只球,其中3只黑球,2只白球,从中一次随机摸出2只球,至少有1只黑球的概率是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.设a,b均为正实数,则
正确答案
4
解析
解析已在路上飞奔,马上就到!
知识点
12.在平面直角坐标系xOy中,点M是椭圆
正确答案
(0,
解析
解析已在路上飞奔,马上就到!
知识点
13.对于定义域内的任意实数x,函数f(x)=
正确答案
-7<a≤0或a=2
解析
解析已在路上飞奔,马上就到!
知识点
14.记数列{an}的前n项和为Sn,若不等式
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.在△ABC中,已知∠BAC=90°,AB=6,若D点在斜边BC上,CD=2DB,则
正确答案
24
解析
解析已在路上飞奔,马上就到!
知识点
15.在△ABC中,角A,B,C的对边分别为a,b,c,且
(1)求角
(2)若角




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.在四棱锥P-ABCD中,∠ACD=90°,∠BAC=∠CAD,PA⊥平面ABCD,E为PD的中点。
(1)求证:平面PAC⊥平面PCD;
(2)求证:CE//平面PAB。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知数列{an}是等差数列,{bn}是等比数列,且满足a1+a2+a3=9,b1b2b3=27。
(1)若a4=b3,b4-b3=m
①当m=18时,求数列{an}和{bn}的通项公式;
②若数列{bn}是唯一的,求m的值;
(2)若a1+b1,a2+b2,a3+b3均为正整数,且成等比数列,求数列{an}的公差d的最大值。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.在平面直角坐标系xOy中,已知椭圆
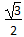
(1)求实数a,b的值;
(2)当直线MN的斜率为1时,若椭圆上恰有两个点P1,P2使得△P1MN和△P2MN的面积为S,求S的取值范围;

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.设a是实数,函数f(x)=ax2+(a+1)x-2lnx
(1)当a=1时,求函数f(x)的单调区间;
(2)当a=2时,过原点O作曲线y=f(x)的切线,求切点的横坐标;
(3)设定义在D上的函数y=g(x)在点P(x0,y0)处的切线方程为l:y=h(x),当x≠x0 时,若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.【选做题】在A、B、C、D四小题中只能选做2题。解答应写出文字说明、证明过程或演算步骤。
A.几何证明选讲
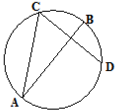
如图,设AB、CD是圆O的两条弦,直线AB是线段CD的垂直平分线。已知AB=6,CD=
B.矩阵与变换
设矩阵A=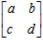




C.坐标系与参数方程
在平面直角坐标系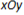



D.不等式选讲
设a,b,c均为正数,abc=1,求证: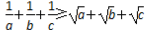
正确答案
A.选修4—1:几何证明选讲
B.选修4—2:矩阵与变换
C.选修4—4:坐标系与参数方程
D.选修4—5:不等式选讲
解析
解析已在路上飞奔,马上就到!
知识点
22.在一个盒子中放有大小质量相同的四个小球,标号分别为1,2,3,4,现从这个盒子中有放回地先后摸出两个小球,它们的标号分别为x,y,记ξ=|x-y|。
(1)求P(ξ=1);
(2)求随机变量ξ的分布列和数学期望。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
23.有三种卡片分别写有数字1,10和100。设m为正整数,从上述三种卡片中选取若干张,使得这些卡片上的数字之和为m。考虑不同的选法种数,例如当m=11时,有如下两种选法:“一张卡片写有1,另一张卡片写有10”或“11张写有1的卡片”,则选法种数为2。
(1)若m=100,直接写出选法种数;
(2)设n为正整数,记所选卡片的数字和为100n的选法种数为an 当n≥2时,求数列{an}的通项公式。
正确答案
解析
解析已在路上飞奔,马上就到!